Методом Крамера. Пусть дана система уравнений вида

Пусть дана система уравнений вида

Введем в рассмотрение следующие определители: ;

; ; .

При решении системы возможны следующие случаи.

1. Если , то данная система имеет единственное решение ; его можно найти по формулам 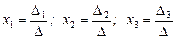, которые называются формулами Крамера.

2. Если , то решить данную систему методом Крамера нельзя.

В этом случае система или не имеет решений (такая система называется несовместной) или имеет бесконечное множество решений (такая система называется неопределенной). Для более детального исследования и нахождения общего решения системы можно использовать, например, метод Гаусса.

Пример. Решить систему уравнений:

Решение. Сначала вычислим главный определитель системы:

Так как , то данную систему можно решить по формулам Крамера.

Вычислим остальные определители:

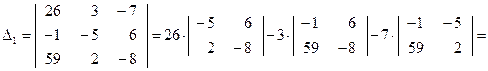
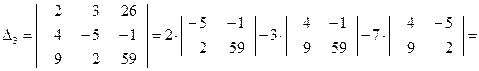
Теперь по формулам Крамера находим:

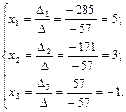
Ответ: .