
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Переход от одной формы комплексного числа к другой
Комплексное число представимо в одной из трех форм:
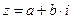 –алгебраическая форма комплексного числа;
–алгебраическая форма комплексного числа;
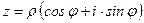 –тригонометрическая форма комплексного числа;
–тригонометрическая форма комплексного числа;
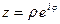 –показательная форма комплексного числа.
–показательная форма комплексного числа.
Если комплексное число задано в показательной или тригонометрической форме, то его действительную и мнимую части можно найти по формулам 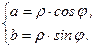
Если комплексное число задано в алгебраической форме, то его модуль можно найти по формуле  , а аргумент –по таблице 1, приведенной в параграфе 2.
, а аргумент –по таблице 1, приведенной в параграфе 2.
Пример 11. Представить данное число 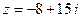 в тригонометрической и показательной форме, найти его действительную и мнимую части, модуль и аргумент.
в тригонометрической и показательной форме, найти его действительную и мнимую части, модуль и аргумент.
Решение. Число задано в алгебраической форме. Из условия находим действительную и мнимую части числа:  ,
, 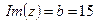 .
.
Найдем модуль и аргумент данного числа:

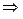
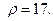
Так как 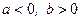 , то для вычисления аргумента в таблице 1 находим формулу
, то для вычисления аргумента в таблице 1 находим формулу 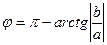 , по которой получаем:
, по которой получаем:

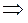
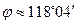
или 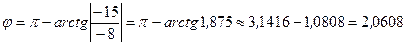 (радиан).
(радиан).
Ответ: Действительная часть числа z  .
.
Мнимая часть числа z  .
.
Модуль числа z 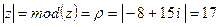 .
.
Аргумент числа z 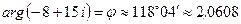 .
.
Тригонометрическая форма числа: 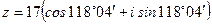 или
или
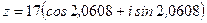 .
.
Показательная форма числа: 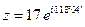 или
или 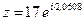 .
.
Указания по вычислению аргумента  с помощью инженерного микрокалькулятора
с помощью инженерного микрокалькулятора
1. Для вычисления значения аргумента  в градусах, минутах и секундах нужно:
в градусах, минутах и секундах нужно:
1) нажатием клавиши DRGвыбрать градусную меру угла (на индикаторе должна появиться запись DEG ‒ градусы);
2) ввести число 1,875;
3) нажать клавиши 2ndF и tan (выполнится команда tan-1, то есть  ); на индикаторе появляется число 61,92751306 – это
); на индикаторе появляется число 61,92751306 – это  , то есть значение угла
, то есть значение угла 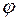 , в градусах и десятичных долях градусов;
, в градусах и десятичных долях градусов;
4) нажать клавиши 2ndF и DEG (выполнится команда →D.MS – перевод градусов и их десятичных долей в градусы, минуты и секунды). На индикаторе появляется число 61,55390470 – это значение угла 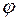 в градусах, минутах и секундах: целая часть числа – это количество градусов, первая и вторая цифры дробной части – это количество минут, третья и четвертая цифры дробной части – это количество секунд. Таким образом,
в градусах, минутах и секундах: целая часть числа – это количество градусов, первая и вторая цифры дробной части – это количество минут, третья и четвертая цифры дробной части – это количество секунд. Таким образом, 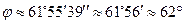 .
.
Замечание. Обычно все вычисления с помощью калькулятора производятся без переписывания промежуточных результатов на бумагу. В данном случае алгоритм вычисления аргумента такой (каждая ячейка таблицы обозначает клавишу МК):
| / | = | 2ndF | tan | +/‒ | + | = | 2ndF | DEG |
| Алгоритм вычисления модуля числа имеет вид: | x2 | + | x2 | = | √ |
2. Чтобы вычислить значение аргумента  в радианах, нужно:
в радианах, нужно:
1) нажатием клавиши DRGвыбрать радианную меру угла (на индикаторе должна появиться запись RAD – радианы);
2) набрать число 1,875;
3) нажать клавиши 2ndF и tan (выполнится команда tan-1, то есть  ). На индикаторе появляется число 1,08083900– это значение угла
). На индикаторе появляется число 1,08083900– это значение угла 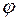 в радианах. Его можно округлить с желаемой степенью точности. Например,
в радианах. Его можно округлить с желаемой степенью точности. Например,  .
.
Замечание. Алгоритм вычисления аргумента без переписывания промежуточных результатов на бумагу такой:
| / | = | 2ndF | tan | +/‒ | + | 2ndF | EXP | = |
Пояснение. Нажатием клавиш 2ndF и EXP вводят значение константы  .
.
Пример 12. Представить число  в алгебраической и показательной форме, найти его действительную и мнимую части, модуль и аргумент.
в алгебраической и показательной форме, найти его действительную и мнимую части, модуль и аргумент.
Решение. Число задано в тригонометрической форме. Из условия находим его модуль и аргумент: 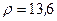 ,
, 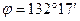 .
.
По формулам  находим действительную и мнимую части данного числа.
находим действительную и мнимую части данного числа.
Получаем:
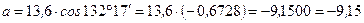 ,
,
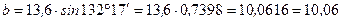 .
.
Ответ: Действительная часть числа  :
: 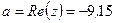 .
.
Мнимая часть числа  :
:  .
.
Модуль числа  :
: 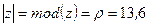 .
.
Аргумент числа  :
: 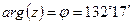 .
.
Показательная форма числа:  .
.
Алгебраическая форма числа: 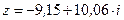
Указания по вычислению значений  и
и 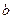 с помощью инженерного микрокалькулятора
с помощью инженерного микрокалькулятора
1) Поскольку аргумент  задан в градусах и минутах, нажатием клавиши DRGвыбрать градусную меру угла (на индикаторе должна появиться запись DEG ‒ градусы).
задан в градусах и минутах, нажатием клавиши DRGвыбрать градусную меру угла (на индикаторе должна появиться запись DEG ‒ градусы).
2) Ввести число 132.17 – это значение аргумента в градусах и минутах.
3) Нажать клавишу DEG . Выполнится команда перевода градусов, минут, секунд в градусы и их десятичные доли; на индикаторе появится число 132,2833333 – это значение аргумента в градусах и десятичных долях градусов.
4) Нажать клавишу cos (вычислится 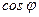 ). На индикаторе появляется число – 0,672797335 (значение
). На индикаторе появляется число – 0,672797335 (значение 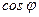 ).
).
5) Не переписывая это число на бумагу, нажать клавишу «умножить»; ввести число 13,6; нажать клавишу «равно»; полученный результат округлить до нужного числа десятичных знаков.
Алгоритм вычисления числа  на МК такой:
на МК такой:
| . | DEG | cos | x | . | = |
Значение 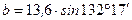 вычисляется точно так же:
вычисляется точно так же:
| . | DEG | sin | x | . | = |
Пример 13. Представить число 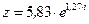 в тригонометрической и алгебраической формах, найти его действительную и мнимую части, модуль и аргумент.
в тригонометрической и алгебраической формах, найти его действительную и мнимую части, модуль и аргумент.
Решение. Число задано в показательной форме. Из условия находим его модуль и аргумент: 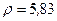 ,
,  (радиан).
(радиан).
Действительную и мнимую части данного числа по формулам:
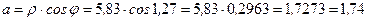 ,
,
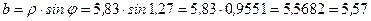 .
.
Ответ: Действительная часть числа  :
:  .
.
Мнимая часть числа  :
: 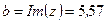 .
.
Модуль числа  :
: 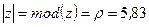 .
.
Аргумент числа  :
: 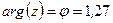 .
.
Тригонометрическая форма числа:  .
.
Алгебраическая форма числа: 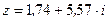 .
.
Указания по вычислению значений  и
и 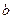 с помощью инженерного микрокалькулятора
с помощью инженерного микрокалькулятора
1) Так как аргумент  задан в радианах, нажатием клавиши DRGвыбрать радианную меру угла (на индикаторе должна появиться запись RAD ‒ радианы).
задан в радианах, нажатием клавиши DRGвыбрать радианную меру угла (на индикаторе должна появиться запись RAD ‒ радианы).
2) Ввести число 1.27 – это значение аргумента в радианах.
3) Нажать клавишу cos (вычислится 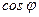 ). На индикаторе появится число 0,296280872 (значение
). На индикаторе появится число 0,296280872 (значение 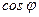 ).
).
4) Не переписывая это число на бумагу, нажать клавишу «умножить»; ввести число 5,83; нажать клавишу «равно»; полученный результат округлить до нужного числа десятичных знаков.
Алгоритм вычисления числа  на МК такой:
на МК такой:
| . | cos | x | . | = |
Значение 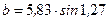 вычисляется точно так же:
вычисляется точно так же:
| . | sin | x | . | = |
Дата добавления: 2015-04-18; просмотров: 1891; Мы поможем в написании вашей работы!; Нарушение авторских прав |