Отношения. Свойства отношений

Отношения — один из способов задания взаимосвязей между элементами множества. Наиболее изученными являются унарные и бинарные отношения.

Унарные (одноместные) отношения отражают наличие какого-то определенного свойства R у элемента множества М. Тогда все элементы a из множества M, которые обладают свойством R, образуют некоторое подмножество, называемое унарным отношением R.

Бинарные (двуместные) отношения используются для определения взаимосвязей, которыми характеризуются пары элементов множества М. Тогда все пары элементов множества M, между которыми существует отношение R, образуют подмножество R множества 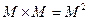всех возможных пар элементов. Это подмножество называется бинарным отношением R.

В общем случае рассматриваются n-местные отношения, например, тернарные отношения—отношения между тройками элементов.

Рассмотрим более подробно бинарные отношения. Если бинарное отношение R задается между парами элементов двух различных множеств 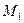и , тогда отношение R образует множество пар прямого произведения .

Множество 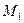называется областью определения D(R) отношения R: .

Множество называется множеством значений Q(R) отношения R: .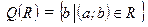

Бинарные отношения могут быть заданы любыми способами задания множеств. На конечных множествах бинарные отношения обычно задаются:

1. Перечислением пар, для которых это отношение выполняется.

2. Матрицей. Бинарному отношению 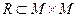, где , соответствует квадратная матрица порядка n, в которой элемент 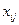определяется условием