
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывность суммы, произведения, частного двух функций
Определение 1. Число  называется левым пределом функции
называется левым пределом функции  при
при  , если для всех значений х, достаточно близких к
, если для всех значений х, достаточно близких к 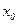 и меньших, чем
и меньших, чем 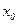 , значения
, значения  как угодно мало отличаются от
как угодно мало отличаются от  .
.
Определение 2. Число  называется правым пределом функции
называется правым пределом функции  при
при  , если для всех значений х, достаточно близких к
, если для всех значений х, достаточно близких к 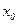 и больших, чем
и больших, чем 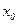 , значения
, значения  как угодно мало отличаются от
как угодно мало отличаются от  .
.
Обозначения: 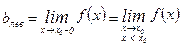 ;
; 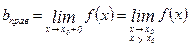 .
.
Определение 3.Функция  называется непрерывной в точке
называется непрерывной в точке 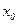 , если левый и правый пределы
, если левый и правый пределы  при
при  конечные, равны между собой и равны значению функции
конечные, равны между собой и равны значению функции  в точке
в точке 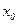 :
: 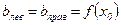 .
.
Определение 4. Функция f(x) называется непрерывной на данном промежутке, если она непрерывна в каждой точке этого промежутка.
Теорема 1. Если функции  и
и  непрерывны на промежутке
непрерывны на промежутке  , то функция
, то функция  тоже непрерывна на промежутке
тоже непрерывна на промежутке  .
.
Теорема 2. Если функции  и
и  непрерывны на промежутке
непрерывны на промежутке  , то функция
, то функция  тоже непрерывна на промежутке
тоже непрерывна на промежутке  .
.
Теорема 3. Если данные функции  и
и  непрерывны на промежутке
непрерывны на промежутке  и
и 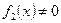 на промежутке
на промежутке  , то функция
, то функция 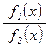 тоже непрерывна на промежутке
тоже непрерывна на промежутке  .
.
Пример 1. Исследовать на непрерывность и точки разрыва функцию

Решение. Так как на промежутках 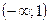 и
и 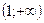 данная функция совпадает с непрерывными функциями,
данная функция совпадает с непрерывными функциями, 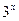 и
и  , то она непрерывна на этих промежутках.
, то она непрерывна на этих промежутках.
Чтобы установить, является ли точка  точкой разрыва, и определить тип разрыва, вычислим пределы:
точкой разрыва, и определить тип разрыва, вычислим пределы:
 ,
,  .
.
Теперь вычислим значение функции в точке  :
:  .
.
Так как  , то в точке
, то в точке  функция непрерывна.
функция непрерывна.
Ответ.Данная функция непрерывна на промежутке 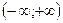 .
.
Дата добавления: 2015-04-18; просмотров: 320; Мы поможем в написании вашей работы!; Нарушение авторских прав |