
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Виды дедуктивных рассуждений
Математика как наука и учебный предмет в школе
Метод математической индукции; аксиоматический метод; метод "от противного"
1.
I: Отметьте один правильный ответ.
S: В методике преподавания математики аксиоматический метод используется как способ:
А) доказательства;
Б) решения задачи;
В) введения понятий;
Г) построения теории;
Д) поиска плана решения задачи.
Ответ: Г.
2.
I: Вставьте в предложение пропущенное слово.
S: В школьном курсе математики аксиоматический метод используется как способ _________ теории.
Ответ: построения (Построения, изложения, Изложения)
3.
I: Отметьте один правильный ответ.
S: Доказательство методом математической индукции содержит:
А) один шаг;
Б) два шага;
В) три шага;
Г) четыре шага;
Д) пять шагов.
Ответ: В
4.
I: Отметьте один правильный ответ.
Большей посылкой в доказательстве утверждения методом математической индукции является принцип … индукции. Пропущено слово:
А) аксиоматической;
Б) математической;
В) неполной;
Г) полной;
Д) прямой.
Ответ: Б.
5.
I: Установите последовательность шагов доказательства методом математической индукции
S: Выберите нужные предложения, входящие в доказательство истинности утверждения P(n) для N, и укажите порядок их следования.
- Доказывают истинность P(n) для n = k+1.
- Допускают истинность утверждения P(n) для n = k.
- Из допущения истинности P(n) для n = k, выводят истинность P(n) для n = k+1.
- На основе истинности P(1) и
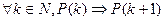 выводят
выводят 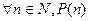 .
. - Проверяют истинность утверждения P(n) для n = 1.
Ответ: 534 (5,3,4; 5;3;4)
5 и 6 — ОДНО И ТОЖЕ, ТОЛЬКО 5 было с ошибкой (без формул)
6.
I: Установите последовательность шагов доказательства методом математической индукции
S: Выберите нужные предложения, входящие в доказательство утверждения P(n): для  N, и укажите порядок их следования.
N, и укажите порядок их следования.
1. Доказывают истинность P(n) для n = k+1.
2. Допускают истинность утверждения P(n) для n = k.
3. Из допущения истинности P(n) для n = k, выводят истинность P(n) для n = k+1.
4. На основе истинности P(1) и 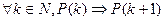 выводят
выводят 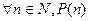 .
.
5. Проверяют истинность утверждения P(n) для n = 1.
Ответ: 534 (5,3,4 5;3;4 5.3.4.)
6.Установите последовательность шагов доказательства методом математической индукции
| № п/п | Инструкция: Выберите нужные предложения, входящие в доказательство утверждения P(n):  , и укажите порядок их следования. , и укажите порядок их следования.
|
| 1. | Выводят: ( 
|
| 2. | Доказывают истинность  . .
|
| 3. | Из допущения истинности  , выводят , выводят  . .
|
| 4. | На основе P(1) и 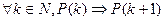 выводят выводят  . .
|
| 5. | Предполагается истинность утверждения  . .
|
| 6. | Проверяется истинность утверждения P(1) . |
Ответ: 634 (6,3,4 6;3;4 6.3.4.)
I: Вставьте пропущенное слово в предложении.
S: Большей посылкой в доказательстве утверждения методом математической индукции является принцип ______________ индукции.
Ответ: математической (Математической).
8.
I: Отметьте один правильный ответ.
S: «От противного» является видом следующего метода доказательства:
А) аналитического;
Б) дедуктивного;
В) косвенного;
Г) обратного;
Д) прямого.
Ответ: В.
9.
I: Установите соответствие:
L1: Аксиоматический
L2: «От противного»
L3: Математической индукции
R1: Используется для выдвижения гипотезы
R2: Используется как способ построения теории
R3: Применяется для утверждений P(n),  N
N
R4: Является видом косвенного доказательства
10.
I: Вставьте пропущенное слово в предложении.
S: Доказательство методом «от противного» основано на эквивалентности двух теорем: прямой и ________________ к обратной.
Ответ: противоположной (Противоположной)
Дата добавления: 2015-04-18; просмотров: 258; Мы поможем в написании вашей работы!; Нарушение авторских прав |