Алгоритм БПФ.

Рассмотрим алгоритм быстрого преобразования Фурье: сущность алгоритма сводится к многократному делению заданной последовательности отсчетов сигнала на более короткие последовательности и нахождению дискретного преобразования Фурье массивов с меньшим числом членов, где 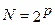– число отсчетов, – целое число, исходный сигнал.

Рис.1.1.Дискретное преобразование Фурье.

Разобьем исходную последовательность(см.рис.1.1.) 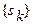на две: четную и нечетную (см.рис.1.2.), где , .

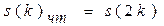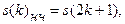
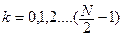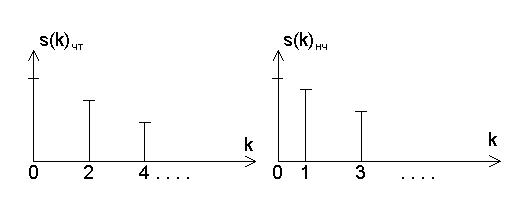
Рис.1.2.Четная и нечетная последовательность.

Таким образом дискретное преобразование Фурье примет вид

Из этого выражения видно, что первая половина коэффициентов дискретного преобразования Фурье с номером от 0 до 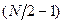выражается через коэффициент дискретного преобразования Фурье 2-х частных последовательностей, то есть (1.1.)

Учтем, что последовательности коэффициентов, относящихся к четной и нечетной частям исходного сигнала, являются периодическими с 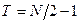, то есть

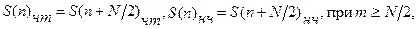(1.2.)

Где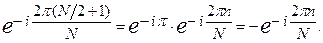

Таким образом 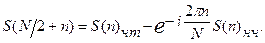(1.3.)

Далее вычисление строится по алгоритму: последовательности с четными и нечетными номерами разбивается на части, также четные и нечетные, и так далее, пока не получим последовательность из одного элемента. Для работы с этим алгоритмом в компьютер необходимо внести весь массив.