
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм линейной цифровой фильтрации. Условие физической реализуемости.
Математическая теория цифровых фильтров переносит на случай дискретных сигналов все основные положения теории линейных систем, преобразующих непрерывные сигналы.
Как известно, линейная стационарная система преобразует непрерывный входной сигнал х(t) таким образом, что на ее выходе возникает колебание y(t) равное свертке функции х(t) и импульсной характеристики h(t):

Линейный цифровой фильтр, по определению, есть дискретная система (физическое устройство или программа для компьютера), которая преобразует последовательность 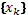 числовых отсчетов входного сигнала в последовательность
числовых отсчетов входного сигнала в последовательность  отсчетов выходного сигнала:
отсчетов выходного сигнала:
 (2.126)
(2.126)
или сокращенно
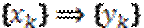
Линейный цифровой фильтр обладает тем свойством, что сумма любого числа входных сигналов, умноженных на произвольные коэффициенты, преобразуется в сумму его откликов на отдельные слагаемые, т. е. из соответствий

следует, что
 (2.127)
(2.127)
при любых коэффициентах  .
.
Для того чтобы обобщить формулу (2.125) на случай дискретных сигналов, вводят понятие импульсной характеристики ЦФ. По определению, она представляет собой дискретный сигнал {hk}, который является реакцией ЦФ на «единичный импульс»  :
:
 (2.128)
(2.128)
Линейный ЦФ стационарен, если при смещении входного единичного импульса на любое число интервалов дискретизации импульсная характеристика смещается таким же образом, не изменяясь по форме. Например:

 (2.129)
(2.129)
. . . . . . . . . . . . . . . . . . .
Рассмотрим, каким образом из свойств линейности и стационарности вытекает наиболее общий алгоритм линейной цифровой фильтрации. Пусть  — некоторый сигнал на входе ЦФ с известной импульсной характеристикой. Используя соотношения (2.127) и (2.129), можно записать т-й отсчет выходного сигнала
— некоторый сигнал на входе ЦФ с известной импульсной характеристикой. Используя соотношения (2.127) и (2.129), можно записать т-й отсчет выходного сигнала 

Формула (2.130), играющая ведущую роль в теории линейной цифровой фильтрации, показывает, что выходная последовательность есть дискретная свертка входного сигнала и импульсной характеристики фильтра. Смысл этой формулы прост и нагляден: в момент каждого отсчета ЦФ проводит операцию взвешенного суммирования всех предыдущих значений входного сигнала, причем роль последовательности весовых коэффициентов играют отсчеты импульсной характеристики. Иными словами, ЦФ обладает некоторой «памятью» по отношению к прошлым входным воздействиям.
Практический интерес представляют лишь физически реализуемые ЦФ, импульсная характеристика которых не может стать отличной от нуля в отсчетных точках, предшествующих моменту подачи входного импульса. Поэтому для физически реализуемых фильтров коэффициенты 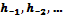 обращаются в нуль и суммирование в (2.130) можно распространить на все положительные значения индекса k:
обращаются в нуль и суммирование в (2.130) можно распространить на все положительные значения индекса k:
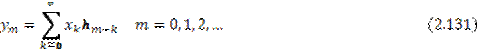
Дата добавления: 2015-04-21; просмотров: 318; Мы поможем в написании вашей работы!; Нарушение авторских прав |