
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рекурсивный ЦФ. Канонические схемы ЦФ.
Конструкция РЦФ отображается в z-образе передаточной функции фильтра в виде отношения двух многочленов:
H(z) = H0+H1z+H2z2+...= B(z)/[1+A(z)], (9.1.1)
где: B(z) = B0+B1z+B2z2+ ... +BNzN, A(z) = A1z+A2z2+ ... +AMzM.
Естественно, что переход на РЦФ имеет смысл только в том случае, если степень многочленов A(z) и B(z) во много раз меньше степени многочлена H(z) прямого z-преобразования импульсной реакции фильтра. При z-образе входных данных Х(z), на выходе РЦФ имеем:
Y(z) = H(z)Х(z) = X(z)B(z)/[1+A(z)], Y(z)[1+A(z)] = Y(z)+Y(z)A(z) = X(z)B(z), Y(z) = X(z)B(z)-Y(z)A(z). (9.1.2)
При обратном z-преобразовании выражения (9.1.2) получаем уравнение рекурсивной цифровой фильтрации: yk = 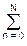 bn xk-n –
bn xk-n – 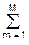 am yk-m. (9.1.3)
am yk-m. (9.1.3)
Рекурсивная фильтрация требует задания начальных условий как по xk, так и по yk при k<0. Схема рекурсивной фильтрации приведена на рис. 9.1.1.
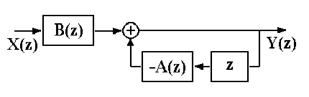 Рис. 9.1.1. Схема РЦФ. Рис. 9.1.1. Схема РЦФ.
|
Как следует из выражения (9.1.3), при вычислении значения уk текущей точки используются предыдущие вычисленные значения yk-m, (m>0), что и определяет принцип рекурсии - фильтрации с обратной связью. Другой особенностью РЦФ является их односторонность и физическая реализуемость в реальном масштабе времени. При машинной обработке данных многочлен B(z) передаточной функции фильтра может реализоваться и в двухстороннем варианте.
Одно из важнейших свойств рекурсивных фильтров - возможность получения узких переходных зон при конструировании частотных фильтров, так как функция H(z) фильтра может резко изменяться при приближении к нулю (но не нулевого) многочлена в знаменателе (9.1.1).
Рекурсивная фильтрация требует более высокой точности вычислений по сравнению с нерекурсивной, т.к. использование предыдущих выходных отсчетов для текущих вычислений может приводить к накапливанию ошибок. Особое значение это имеет для фильтров с передаточными функциями высоких порядков (M>3), которые чувствительны к эффектам конечной разрядности. Такие фильтры, как правило, разбиваются на фрагменты – звенья второго и/или первого порядка, и реализуются в каскадной или в параллельной форме.
 Рис. 9.1.2. Каскадная форма РЦФ.
Рис. 9.1.2. Каскадная форма РЦФ.
|
Каскадная форма. Находятся корни многочленов А(z), B(z) и производится разложение H(z):
H(z) =  , (9.1.4)
, (9.1.4)
где G - масштабный множитель. Это позволяет применять каскадное построение фильтров, показанное на рис. 9.1.2, в котором:
H(z) = G H1(z) H2(z) ..... HN(z),
Hn(z) = Bn(z)/An(z). (9.1.5)
Функции Аn(z) и Bn(z) обычно представляются в виде биквадратных блоков (фильтров второго порядка):
Bn(z) = bn.0 + bn.1 z + bn.2 z2, An(z) = 1 + an.1 z + an.2 z2.
В принципе, порядок расположения блоков в каскадной форме, равно как и порядок множителей B(z) и A(z) в числителе и знаменателе функции (9.1.4), значения не имеет. Однако следует учитывать, что полюса знаменателя, близкие к единичной окружности на z-плоскости (близкие по модулю к 1), формируют большие коэффициенты усиления на соответствующих частотах (в блоках, в которых они находятся), и при обработке сигналов могут вызывать переполнение разрядов числовых ячеек этих блоков, если их разрядность ограничена. С учетом этого при формировании каскадов желательно объединять в пары Bi(z)/Ai(z) нули и полюса, близкие по модулю к 1, и располагать их в концевые блоки каскадной схемы. Такое комбинирование полезно также с позиций наилучшего отношения сигнал/шум в выходном сигнале.
 Рис. 9.1.3. Параллельная форма РЦФ.
Рис. 9.1.3. Параллельная форма РЦФ.
|
Параллельная форма. Функция H(z) разлагается на элементарные дроби:
H(z) = Ho(z) 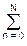 Bn(z) / [1+An(z)],
Bn(z) / [1+An(z)],
что дает параллельную форму фильтра, показанную на рис. 9.1.3. Параллельная конструкция фильтра применяется реже каскадной, хотя это может объясняться и тем, что в аналоговых фильтрах, исторически предшествовавших цифровым фильтрам, теоретическая база анализа и синтеза каскадных рекурсивных фильтров получила детальное развитие.
Стандартные блоки рекурсивных фильтров обычно реализуются биквадратными звеньями в канонической форме, которая имеет минимальное количество элементов задержки. Уравнения звена:
v(k) = x(k) – 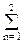 a(n) v(k-n), y(k) =
a(n) v(k-n), y(k) = 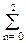 b(n) v(k-n). (9.1.6)
b(n) v(k-n). (9.1.6)
Функциональная схема реализации звена приведена на рис. 9.1.4.
Вторая форма реализации – по уравнению (9.1.5) в прямой форме, приведенная на рис. 9.1.5:
y(k)= 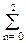 b(n)x(k-n) –
b(n)x(k-n) – 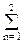 a(n)y(k-n). (9.1.7)
a(n)y(k-n). (9.1.7)
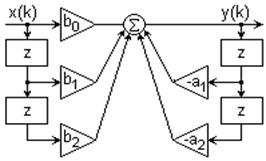 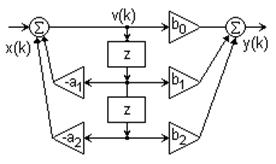 Рис. 9.1.4. Каноническая форма Рис. 9.1.5. Прямая форма
Рис. 9.1.4. Каноническая форма Рис. 9.1.5. Прямая форма
|
При определенных условиях прямая форма лучше канонической с точки зрения шумовых характеристик.
При нулевых значениях коэффициентов a2 и b2 звенья второго порядка превращаются в звенья первого порядка.
Устранение сдвига фазы. Рекурсивные фильтры являются фазосдвигающими фильтрами. Если требуется обеспечить нулевой фазовый сдвиг, то операция фильтрации производится дважды, в прямом и обратном направлении числовой последовательности массива данных, при этом амплитудно-частотная характеристика (АЧХ) фильтрации будет равна |H(w)|2 фильтра, что необходимо учитывать при конструировании фильтра.
Дата добавления: 2015-04-21; просмотров: 301; Мы поможем в написании вашей работы!; Нарушение авторских прав |