Прямое и обратное Z-преобразование. Свойства Z-преобразования.

Прямое z-преобразование. Если задана дискретная числовая последовательность

{x_k}=(x₀, x₁…x_n),

И ей поставить в соответствие сумму ряда по отрицательным степеням комплексной переменной z

z = e^pt, то x(z)= x₀∙z⁰ + x₁∙z ^-1 + … x_m∙z ^-m, (1.1)

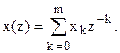
Эта сумма называется z- преобразованием последовательности x^k. Целесообразность z-преобразования при исследовании дискретных цепей обусловлена тем, что основные их свойства можно изучать, исследуя z-преобразования обычными методами матанализа.

Если число членов в ряде (1.1) бесконечно, то необходимо исследовать сходимость ряда. Из теории функции комплексного переменного известно: если коэффициенты ряда (1.1) удовлетворяют условию ,

при необходимых значения k, то ряд (1.1) сходится при всех значениях . В этой области сходимость суммы ряда представляет собой функцию переменной z не имеющей ни полюсов, ни существенно особых точек. Пусть {x_k} = (1, a, a², a³, …), тогда

(1.2)

Обратное z-преобразовани.Пусть функция x(z), где z комплексная переменная по области . Умножим правую и левую часть выражения (1.1) на z^m-1, тогда 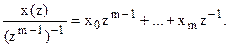(1.3)

Возьмем интеграл по замкнутому контору, лежащему целиком в области аналитичности функции x(z) и охватывающему все полюса функции. Используя теорему Коши, получим (1.4)

Основные свойства преобразования.Линейность.

{x_k}→x(z)

{y_k}→y(z)

{f_k}=α{x_k}+β{y_k}, тогда (F_k)→αX(Z)+βY(Z).

1. Смещение или запаздывание сигнала.

Пусть последовательность {y_k} получается из последовательности {x_k} путем задержки последовательности {x_k} на один шаг: y_k = x_k-1, тогда z – преобразование имеет вид Y(z) = Z ^-1X(Z).

2. z-преобразование свертки. f(t), x(t), y(t) и , тогда F(iω) = X(iω)∙Y(iω)