Частный коэффициент передачи цифрового фильтра и его связь с системной функцией Н(z).Нормировка оси частот.

В теории линейных систем особую роль играют сигналы следующего вида

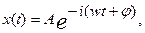(1.1.)

(1.2.)

где ∆- шаг дискретизации по t, k- количество отсчетов.

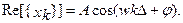(1.3.)

Отсчеты взятые из такого гармонического сигнала называются гармонической последовательностью. Предположим, что есть цифровой фильтр с импульсной характеристикой И на вход такого фильтра подана гармоническая последовательность неограниченно протяженная во времени. Тогда воспользуемся дискретной сверткой чтобы найти выходной сигнал

(1.4.)

Если за знак суммы вынести множитель 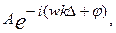то получим выражение

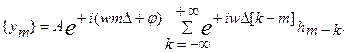(1.5.)

Введем новый индекс (1.6)

тогда

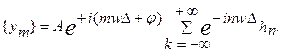(1.7.)

Входной сигнал с частотой и выходной сигнал (на выходе фильтра) имеют одну и ту же структуру дискретной гармонической последовательности. выходной сигнал на выходе цифрового фильтра представляет собой временные отсчеты входного сигнала умноженные на 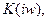где

(1.8.)

Таким образом является периодической функцией частоты с периодом 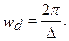есть преобразование Фурье импульсной характеристики цифрового фильтра. Частотную характеристику цифрового фильтра удобно находить, используя z- преобразование

(1.9.)

Системная функция фильтра (коэффициент передачи в z- плоскости) имеет вид

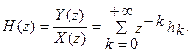(1.10.)

Чтобы перейти от системной функции к коэффициенту передачи произведем замну

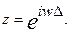(1.11.)