Понятие устойчивости ЦФ и критерий устойчивости.

Фильтр называется устойчивым, если при любых начальных условиях реакция фильтра y(nT) на любое ограниченное воздействие x(nT) также ограничена, т.е. если |x(nT)| ≤ M_x < ∞ для всех n = 0, 1, 2, …, то |y(nT)| ≤ M_y < ∞ для всех n, причем M_x и M_y – постоянные, не зависящие от n. Из уравнения дискретного фильтра следует, что если x(nT) ограничено, т.е. |x(nT)| ≤ M_x < ∞ для всех n, то абсолютное значение выходного сигнала также ограничено:

.

Следовательно, критерием устойчивости дискретного фильтра является абсолютная сходимость ряда отсчетов импульсной характеристики

Можно показать, что данное условие является не только достаточным, но и необходимым условием устойчивости фильтра. Однако непосредственное применение этого условия для проверки устойчивости практически затруднено. Поэтому рассмотрим другую формулировку критерия устойчивости.

В общем случае передаточная функция линейного дискретного фильтра представляется в виде 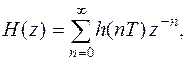поэтому .

Если |z ^–1| ≤ 1, т.е. |z ^–n| ≤ 1, то . Это значит, что в устойчивой системе H(z) конечна во всех точках z-плоскости, где |z| ≥ 1, и, следовательно, передаточная функция H(z) не должна иметь особых точек (полюсов) при z ≥ 1 (на и вне единичной окружности в z-плоскости). Таким образом, система будет устойчива тогда и только тогда, когда все полюсы H(z) расположены внутри единичной окружности в z-плоскости. Если H(z) – дробно-рациональная функция, то полюсы H(z) определяются нулями (корнями) многочлена знаменателя передаточной функции или характеристическим уравнением: , .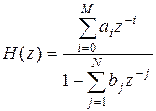

Примеры.

1. Пусть . Полюс H(z) – корень знаменателя z₁ = 0,2 < 1. Таким образом, цифровой фильтр устойчив.

2. Пусть ; здесь корень знаменателя z₁ = –1,2 , т.е. |z₁| > 1, следовательно, фильтр неустойчив.

Заметим, что формулировка критерия устойчивости относится к несократимой дроби, так как возможно, что полюс компенсируется нулем передаточной функции. Например, фильтр, описываемый функцией , устойчив, несмотря на то, что полюс |z| = =1 лежит на единичной окружности; устойчивость фильтра обусловлена тем, что в действительности после сокращения числителя и знаменателя на множитель 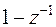получается 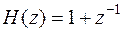. Нерекурсивные фильтры всегда устойчивы, так как все полюсы их передаточной функции локализованы в точке .

31. Синтез ЦФ: метод инвариантных импульсных характеристик и метод дискретизации диф. уравнения аналоговой цепи.

Метод инвариантных импульсных характеристик.

В основе этого метода лежит предположение о том, что синтезируемый ЦФ должен обладать импульсной характеристикой, которая является результатом дискретизации импульсной характеристики соответствующего аналогового фильтра-прототипа. Имея в виду синтез физически реализуемых систем, для которых импульсная характеристика обращается в нуль при t<0,получим следующее выражение импульсной характеристики ЦФ:

,

где T - шаг дискретизации по времени.

Следует обратить внимание на то, что число отдельных членов в выражении импульсной характеристики ЦФ может быть как конечным, так и бесконечным. Это определяет структура синтезируемого фильтра: импульсной характеристике с конечным числом отсчетов отвечает трансверсальный фильтр, в то время как для реализации неограниченно протяженной импульсной характеристики требуется рекурсивный ЦФ.

Связь между коэффициентом импульсной характеристики и структурой ЦФ особенно проста для транверсального фильтра. В общем случае синтез структуры фильтра осуществляется путем применения z-преобразования к последовательности вида приведенного выше. Найдя системную функцию H(z) фильтра, следует сравнить ее с общим выражением и определить коэффициенты транверсальной и рекурсивной частей. Степень приближения амплитудно-частотной характеристики синтезированного ЦФ к характеристике аналогового прототипа зависит от выбранного шага дискретизации. При необходимости следует вычислить частотный коэффициент передачи ЦФ, осуществив в системной функции H(z) замену переменной по формуле , и затем сравнить результат с частотным коэффициентом передачи аналоговой цепи.