Соединение фильтров. Трансверсальный ЦФ. Свойства частотного коэффициента передачи.

Физически осуществимые ЦФ, которые работают в реаль­ном масштабе времени, для формирования выходного сигна­ла в i-й дискретный момент времени могут использовать следующие данные: а) значение входного сигнала в момент i-го отсчета, а также некоторое число «прошлых» входных отсчетов 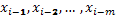; б) некоторое число предшест­вующих отсчетов выходного сигнала Целые числа m и n определяют порядок ЦФ. Классификация ЦФ проводится по-разному в зависимости от того, как используется информация о прошлых состояниях системы.

Траисверсальные ЦФ. Так принято называть фильтры, которые работают в соответствии с алгоритмом

(2.138)

где — последовательность коэффициентов.

Число т является порядком трансверсального цифрового фильтра. Как видно из формулы (2.138), трансверсальный фильтр проводит взвешенное суммирование предшествующих отсчетов входного сигнала и не использует прошлые отсчеты выходного сигнала. Применив z-преобразование к обеим частям выражения (2.138), убеждаемся, что

Отсюда следует, что системная функция

является дробно-рациональной функцией z, имеющей m-кратный полюс при z= 0 и т нулей, координаты которых определяются коэффициентами фильтра.

Алгоритм функционирования трансверсального ЦФ пояс­няется структурной схемой, приведенной на рис. 2.17.

Рис. 2.17. Схема построения трансверсального ЦФ

Основными элементами фильтра служат блоки задержки отсчетных значений на один интервал дискретизации (пря­моугольники с символами z^-1), а также масштабные блоки, выполняющие в цифровой форме операции умножения на соответствующие коэффициенты. С выходов масштабных блоков сигналы поступают в сумматор, где, складываясь, образуют отсчет выходного сигнала.

Вид представленной здесь схемы объясняет смысл термина «трансверсальный фильтр» (от англ. transverse — поперечный).

Импульсная характеристика. Вернемся к формуле (2.139) и вычислим импульсную характеристику трансверсального ЦФ, осуществив обратное z-преобразование. Легко видеть, что каждое слагаемое функции H(z) дает вклад, равный соответ­ствующему коэффициенту , смещенному на п позиций в сторону запаздывания. Таким образом, здесь

(2.140)

К такому выводу можно прийти и непосредственно, рас­сматривая структурную схему фильтра (см. рис. 2.17) и пола­гая, что на его вход подан «единичный импульс» (1, 0, 0, 0, ...).

Важно отметить, что импульсная характеристика трансвер­сального фильтра содержит конечное число членов.

Частотная характеристика. Если в формуле (2.139) провести замену переменной , то получим частотный коэф­фициент передачи

(2.141)

При заданном шаге дискретизации А можно реализовать самые разнообразные формы АЧХ, подбирая должным обра­зом весовые коэффициенты фильтра.