Ограниченные и неограниченные последовательности.

Введение в математический анализ. Числовая последовательность.

Числовая последовательность – Функция вида , заданная на множестве N натуральных чисел.
Обозначается в виде {x_n}, . Число x₁ называется первым членом (элементом) последовательности, x_n – общим или n-м членом последовательности.

Задается либо формулой общего члена, либо рекуррентной формулой.

Формула общего члена позволяет вычислить любой член последовательности по номеру n (при помощи этой формулы можно сразу вычислить любой член последовательности).

Пример:

Рекуррентная формула определяет правило, по которому можно найти n-ый член последовательности, зная первый и (n-1)-ый члены (при таком способе для нахождения 100-го члена последовательности придётся сначала посчитать 99 предыдущих).

Ограниченные и неограниченные последовательности.

Числовая последовательность – Функция вида , заданная на множестве N натуральных чисел.
Обозначается в виде {x_n}, . Число x₁ называется первым членом (элементом) последовательности, x_n – общим или n-м членом последовательности.

Последовательность {x_n} называется ограниченной,если существует такое число , что для любого выполняется неравенство 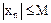. (если , то последовательность - неограниченная).