Свойства бесконечно малых функций.

Функция 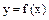называется бесконечно малой при , если .

Алгебраическая сумма б.м.ф. есть б.м.ф.

Пусть и - две б.м.ф. при . Это значит, что , т.е. для любого , а значит, и найдется число , такое, что для всех х, удовлетворяющих неравенству , выполняется неравенство . Тоже самое проделаем для ( , )

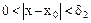Пусть - наименьшее из чисел и 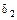. Тогда для всех х, удовлетворяющих неравенству , выполняются неравенства и , следовательно имеет место соотношение 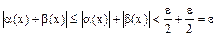, таким образом , т.е. - б.м.ф. при

Произведение ограниченной функции на б.м.ф. есть б.м.ф.

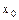Пусть функция ограничена при . Тогда существует такое число , что для всех х -окрестности точки . И пусть - б.м.ф. при . Тогда для любого , а значит и , найдется такое число , что при всех х, удовлетворяющих неравенству 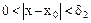, выполняется неравенство

Пусть - наименьшее из чисел и 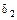. Тогда для всех х, удовлетворяющих неравенству , выполняются неравенства и , следовательно, . А это означает, что - б.м.ф. при