
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства эквивалентных бесконечно малых.
1) Предел отношения двух б.м.ф. не изменится, если каждую из них заменить эквивалентной бесконечно малой.
Пусть 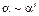 и
и 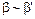 при
при  , тогда
, тогда 
2) Разность б.м.ф. есть б.м.ф. более высокого порядка, чем каждая из них.
Пусть  при
при  , тогда
, тогда  , аналогично
, аналогично 
3) Сумма конечного числа б.м.ф. разных порядков эквивалентна слагаемому низшего порядка.
Пусть  и
и 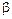 есть б.м.ф. при
есть б.м.ф. при  , причём
, причём  - б.м.ф. высшего порядка, чем
- б.м.ф. высшего порядка, чем 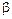 , т.е.
, т.е.  .
.
Тогда  , следовательно,
, следовательно,  при
при  .
.
Первый замечательный предел.
 - первый замечательный предел
- первый замечательный предел
Возьмем круг радиуса 1, обозначим радиальную меру угла MOB через х. Пусть  . На рисунке
. На рисунке  , дуга MB численно равна центральному углу х,
, дуга MB численно равна центральному углу х, 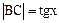 . Очевидно имеем
. Очевидно имеем 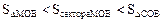 .На основании соответствующих формул геометрии получаем
.На основании соответствующих формул геометрии получаем 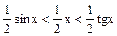 , разделим неравенство на
, разделим неравенство на  , получим
, получим  или
или  . Так как
. Так как 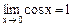 и
и  , то по признаку о пределе промежуточной функции
, то по признаку о пределе промежуточной функции 

Дата добавления: 2015-02-10; просмотров: 274; Мы поможем в написании вашей работы!; Нарушение авторских прав |