Формула Тейлора.

Для многочлена степени n:

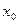Для произвольной функции: Если функция определена в некоторой окрестности точки и имеет в ней производные до -го порядка включительно, то для любого х из этой окрестности найдется точка такая, что справедлива формула:

, где

- остаточный член формулы Тейлора, записанный в форме Лагранджа

Формула Лагранжа.

или

Формула Маклорена.

Частный случай формулы Тейлора при .

, где .

Представление функций по формуле Тейлора.

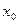Если функция определена в некоторой окрестности точки и имеет в ней производные до -го порядка включительно, то для любого х из этой окрестности найдется точка такая, что справедлива формула:

Бином Ньютона.

Бином Ньютона – формула, выражающая выражение в виде многочлена.

Дата добавления: 2015-02-10; просмотров: 30; Нарушение авторских прав