Применение дифференциала к приближенным вычислениям.

,причем это равенство тем точнее, чем меньше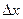

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

Теоремы о среднем.

Теорема Ролля.

Если функция непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), и на концах отрезка принимает одинаковые значения , то найдется хотя бы одна точка 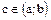, в которой производная обращается в нуль, т.е. .

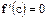Теорема Лагранжа.

Если функция непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), то найдется хотя бы одна точка 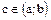такая, что выполняется равенство

Теорема Коши.

Если функции и непрерывны на отрезке [a;b], дифференцируема на интервале (a;b), причем для , то найдется хотя бы одна точка такая, что выполняется равенство .

Дата добавления: 2015-02-10; просмотров: 16; Нарушение авторских прав