Сложение поступательных и вращательных движений

Первый случай. Рассмотрим сначала следующий случай сложного движения: тело Р движется поступательно с постоянной скоростью v₀ относительно системы координат O₂x₂у₂z₂, а она в свою очередь вращается вокруг оси z₁ неподвижной системы координат O₁x₁y₁z₁ с постоянной угловой скоростью ω параллельной скорости v₀ поступательного движения. Найдем абсолютную скорость некоторой точки М тела (рис. 14.10):

Таким образом, абсолютная скорость точки может быть разложена на две составляющие: одну v₀, параллельную оси z₂, и другую v_e = ω × r, перпендикулярную плоскости, проходящей через ось z₁ и точку М.

Отсюда следует, что точка М движется по боковой поверхности кругового цилиндра с осью z₁. Касательная к винтовой траектории образует с плоскостью, перпендикулярной оси цилиндра, угол α, причем

где R — радиус цилиндра (см. рис. 14.10).

Время Т одного оборота тела в винтовом движении

Любая точка тела переместится за это время параллельно оси на расстояние, равное

называемое шагом винта. Величина р = называется параметром винта.

Рассмотренное сложное движение тела называется кинематическим винтом.

Если скоростьv₀ и угловая скорость ω переменны, то движение тела будет мгновенно винтовым движением. Естественно, что параметр винта в общем случае также будет переменным.

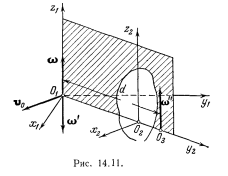Второй случай. Скорость поступательного движения перпендикулярна угловой скорости вращательного движения. Согласно § 14.3 мгновенное поступательное движение можно рассматривать как сложное движение — пару вращений. При этом момент пары вращений должен быть равен скорости данного поступательного движения. Плоскость пары вращений должна быть перпендикулярна v₀ —проведем ее через ось z₁(рис. 14.11). Поступательное движение со скоростью v₀ относительно системы координат O₂x₂у₂z₂ можно заменить вращением тела с угловой скоростью ω" относительно некоторой новой системы и вращением этой новой системы относительно системы координат O₂x₂у₂z₂ с угловой скоростью ω' = − ω". Для упрощения чертежа плоскость у₂O₂z₂ проведена перпендикулярно v₀ через ось z₁. Пусть одно из вращений, составляющих пару, имеет угловую скорость

ω' = − ω и происходит вокруг оси, совпадающей с гг; тогда другое вращение имеет угловую скорость ω" = ω и происходит вокруг параллельной оси, проходящей через точку O₃. Для эквивалентности этой пары вращений данному поступательному движению тела достаточно, чтобы было выполнено условие

Если 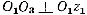(см. рис. 14.11), то отсюда следует, что

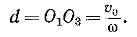
Таким образом, совокупность поступательного и вращательного движений нами приведена к трем вращениям (ω", ω', ω), при этом два последних вращения (ω',ω) эквивалентны покою, так как угловые скорости ω' и ω равны по модулю и направлены по одной прямой в противоположные стороны. Следовательно, результирующее движение эквивалентно только одному вращению вокруг мгновенной оси, проходящей через точку O₃, с угловой скоростью, равной угловой скорости заданного вращения.

Третий случай. Скорость поступательного движения v₀ направлена под углом φ

к угловой скорости ω вращательного движения (рис. 14.12). Этот случай легко приводится к первому. В самом деле, поступательное ставить как совокупность двух поступательных движений со скоростями v₁ и v₂, причем (рис. 14.12) и v₁+v₂ = v₀.

Поступательное движение со скоростью v₂ (в соответствии со вторым случаем) можно заменить парой вращений (ω', ω"). Получилась система четырех движений (v₁, ω", ω', ω); при этом два последних движения (ω',ω) эквивалентны покою, следовательно, остается мгновенно-винтовое движение (v₁, ω").

Если скорости v₀, ω постоянны, то движение будет винтовым. При этом ось винта отстоит от оси z₁ на расстоянии

Шаг винта равен