Общий случай сложения движений твердого тела

Продолжим установленную в §§ 14.4 и 14.5 аналогию между угловыми скоростями и силами, приложенными к твердому телу, 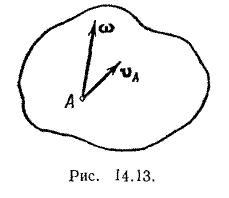а также между скоростью поступательного движения и моментом пары сил.

Эта аналогия объясняется тем, что угловая скорость ω тела и сила, приложенная к твердому телу, являются скользящими векторами. Можно показать (мы не будем останавливаться на доказательстве[1]), что любая система скользящих векторов, независимо от их физической природы, эквивалентна одному скользящему вектору (главному вектору) и одной паре скользящих векторов, момент которой равен главному моменту.

Применительно к сложению движений твердого тела это означает следующее: если тело участвует одновременно в n вращениях с угловыми скоростями ω₁, ω₂, …, ω_n и в m поступательных движениях, скорости которых равны v₁, v₂, ..., v_m (моменты пар вращений), то вся система этих движений эквивалентна совокупности одного вращательного и одного поступательного движений. Угловая скорость ω результирующего вращения равна сумме (главному вектору) составляющих угловых скоростей

^(14.15)

а скорость v_Aрезультирующего поступательного движения равна сумме (главному моменту) моментов угловых скоростей ω_i относительно центра приведения А и скоростей v_i- поступательных движений (моментов пар вращения):

^(14.16)

причем ось вращения проходит через выбранный центр приведения А.

На рис. 14.13 показаны результирующая угловая скорость ω вращательного движения (главный вектор) и результирующая скорость v_A (главный момент) поступательного движения. Векторы v_A и ω можно рассматривать так же, как скорость полюса А и угловую скорость вращения тела относительно полюса

(§ 12.4).

Покажем, что имеются два кинематических инварианта, аналогичных статическим инвариантам. Действительно, из равенства (14.15) следует, что главный вектор ω не зависит от выбора центра приведения А и, следовательно, представляет собой первый кинематический инвариант. По существу, инвариантность главного вектора тождественна с ранее доказанным утверждением о независимости угловой скорости тела от выбора полюса. В более узком смысле под первым инвариантом I₁ будем понимать квадрат модуля главного вектора

I₁ = ω². (14.17)

Прежде чем перейти ко второму инварианту, заметим, что при переходе к новому центру приведения, например точке В, главный момент v_в будет связан с главным моментом v_A относительно старого полюса формулой (рис. 14.14)

v_в = v_A + ω ×ρ. (14.18)

Эту формулу можно получить непосредственно из равенства (14.16). Она также следует из того, что главный момент v_в есть скорость точки В твердого тела и определяется формулой (12.20). Умножим скалярно обе части равенства (14.18) на вектор ю:

v_в •ω = v_A• ω + (ω × ρ) • ω.

I₂ = v• ω (I4.20)

Запишем равенство (14.19) в следующей форме:

^{Если 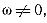то}

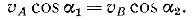
Каждое из этих произведений представляет проекцию главного момента относительно соответствующей точки (скорости соответствующей точки) на направление главного вектора (угловой скорости тела). Следовательно, если угловая скорость тела (главный вектор) не равна нулю, то проекция скорости точки тела (главного момента) на направление угловой скорости тела не зависит от выбора точки.

Покажем, что если второй кинематический инвариант не равен нулю, то совокупность всех движений, в которых участвует тело, может быть сведена к мгновенному винтовому движению. Действительно, если _, то скорость v_A любой точки А тела и угловая скорость его отличны от нуля; кроме того, в этом случае угол а между векторами ω и v_A не равен π/2. На предыдущей было показано, что в этом случае имеется такая точка В, скорость которой v_B параллельна угловой скорости (отела (рис. 14.15). Для этой точки должно выполняться равенство

или, учитывая формулу (14.18),

^(14.21)

где ρ — некоторый скаляр, а ρ—радиус-вектор точки В в системе координат Ахуz, жестко связанной с телом; v_B —скорость точки В.

Очевидно, что равенству (14.21) удовлетворяет радиус-вектор ρ любой точки, лежащей на прямой NN', проходящей через точку В и параллельной вектору ω. Следовательно, равенство (14.21) представляет векторное уравнение прямой линии, все точки которой в данный момент времени имеют скорости, параллельные угловой скорости ω. Прямая NN' называется мгновенной винтовой осью тела; совокупность угловой скорости ω тела и скорости v любой точки мгновенной винтовой оси называется кинематическим винтом, а число ρ в равенстве (14.21) — параметром кинематического винта. Происхождение этих названий очевидно: винтовое движение состоит из вращения вокруг некоторой оси и одновременного поступательного перемещения вдоль этой оси. Таким образом, в самом общем случае скорости точек твердого тела распределяются так, как если бы тело совершала мгновенно-винтовое движение.

* В механике производная по времени обозначается точкой над функцией, так что .

* Доказательства этих утверждений можно найти в любом курсе дифференциальной геометрии.

* Эта формула нам уже знакома (§ 12.4). Скорость, определяемая по этой формуле, есть скорость той точки свободного твердого тела (подвижной системы координат), с которой в данный момент совпадает движущаяся точка.

[1] См , например, Г. К. Суслов, Теоретическая механика, Гостехиздат, 1946, §§ 6—25; Д. Р. Меркин, Алгебра свободных и скользящих векторов, Физматгиз, 1962.