Определение 1.

Задание движения материальной точки в криволинейных координатах.

Ordm;. Понятие криволинейных (обобщенных) координат точки.

Определение 1.

Криволинейными или, иначе, обобщенными координатами материальной точки будем называть три независимые величины , , , которые обладают следующими свойствами.

1. Для любых значений , , из некоторой области 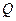трехмерного пространства переменных , , определена однозначная, дважды непрерывно дифференцируемая вектор-функция , такая, что ее векторное значение

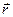= (1)

задает положение материальной точки в абсолютном пространстве при .

2. Для любого положения материальной точки в абсолютном пространстве можно поставить в соответствие одно и только одно значение переменных , , .

3. При любых значениях , , из области 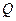смешанное произведение векторов , , 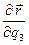не равно нулю, т.е.

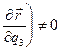, , . (2)

Если задана система отсчета 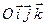, то в скалярной форме соотношение (1) можно записать в виде

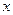= , = , = . (3)

Из сформулированных выше свойств вытекает, что

— функции , , однозначны и дважды непрерывно дифференцируемы;

— система (3) разрешима относительно обобщенных координат , , , так что

= , = , = .

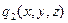Разрешимость следует из теоремы о неявной функции, поскольку якобиан правой части системы (3) отличен от нуля при всех 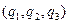из области 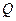. Действительно, матрица Якоби для системы (3) имеет вид:

.

Ее определитель совпадает с левой частью неравенства (2). А потому . Данное неравенство выполняется в любой точке из области 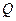. Поэтому из определения 1 обобщенных координат , , следует, что справедливы условия теоремы о неявных функциях для системы уравнений (3), а из самой теоремы вытекает существование решений , , 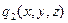этой системы.