Свойство 2.

Векторы , , 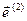линейно независимы, и для смешанного произведения этих векторов справедлива формула

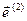( , , ) . (18)

Для доказательства утверждения вычислим сначала векторное произведение векторов 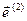и :

= ( ) .

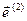
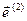
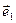
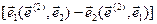В данной записи воспользовались третьей формулой в соотношениях (15) и формулой двойного векторного произведения.

Согласно (17) имеем и . Поэтому окончательно находим

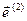
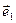. (19)

Подставляя (19) в смешанное произведение векторов , , 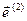и учитывая (17) для , получим

.

Что и требовалось доказать.

Введем косоугольную аффинную систему координат с полюсом в точке и базисными векторами, совпадающими с , , .

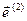Эта система координат называется союзной по отношению к исходной, т.е. основной, системе координат с базисом 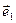, , и полюсом в точке .

Матрицу метрических коэффициентов союзной системы будем обозначать , а элементы этой матрицы — , 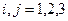. Так что будем иметь:

, , = .

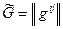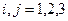Пусть , , — координаты вектора в союзной системе координат, и , , 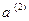— координаты этого вектора в основной системе координат, т.е. его контравариантные координаты.

Покажем, что координаты вектора в союзной системе совпадают с его ковариантными координатами, т.е. справедлива формула

= , . (20)

Действительно, по определению координат вектора в союзной системе можем записать

= .

Умножая это равенство скалярно на 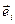, слева (по определению ковариантных координат вектора ) будем иметь

,

где — -я ковариантная координата вектора .

Учитывая (17), справа получим

.

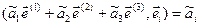Таким образом, равенства (20) доказаны.

Установим связь между матрицам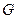и и . А именно, докажем справедливость соотношения

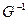= . (21)

Действительно, для любого вектора можем записать

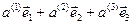= = . (22)

Умножая (22) последовательно (для ) скалярно на 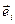, получим

= , .

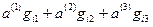Эта система в матричном представлении имеет вид:

. (23)

Умножая (22) последовательно (для ) скалярно на , находим

+ + = , .

Соответственно, в матричном представлении:

= .

Подставляя в левую часть соотношение (23), придем к системе

,

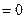где — единичная матрица размерности . В силу произвольности вектора получаем

.

Отсюда следует справедливость соотношения (21).

Докажем следующее утверждение.

Если по заданной исходной основной системе координат построить союзную систему, а затем построенную союзную систему взять в качестве новой основной и построить союзную к ней систему, то эта последняя союзная система будет совпадать с исходной основной системой координат.

Коротко это утверждение формулируется так:

«Союзная система к союзной совпадает с основной».

Утверждение будет доказано, если покажем, что

= ( ) , = ( ) , = ( ) ,

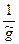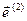
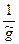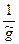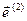где .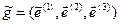

Докажем, например, справедливость первой формулы (остальные — доказываются аналогично).

Выше было установлено (см. (19)) 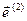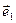. Кроме того, из (18) (свойство 2) имеем . Поэтому для можем записать

= ( ) = ,

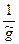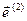
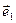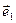что и требовалось доказать.

Из доказанных свойств, в частности, вытекает, что если основной базис является ортонормированным ортогональным базисом, то союзная система координат совпадает с основной. В этом случае ковариантные координаты вектора (величины ) совпадают с соответствующими контравариантными координатами (величинами ).