
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лемма Лагранжа.
При всех  и любых значениях переменных
и любых значениях переменных 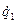 ,
,  ,
,  выполняются равенства
выполняются равенства
а)  =
= 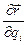 ,
,  ;
;
б)  =
= 
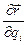 ,
,  .
.
Здесь 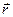 задается формулой (1),
задается формулой (1), 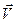 — формулой (31), а
— формулой (31), а 
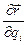 — правой частью равенства (34).
— правой частью равенства (34).
Доказательство.
Равенство а) легко проверяется, поскольку функция 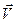 линейно зависит от
линейно зависит от  . Равенство б) проверяется непосредственным вычислением левой и правой части. Вычисляя левую часть равенства б) в формулировке леммы Лагранжа, получим:
. Равенство б) проверяется непосредственным вычислением левой и правой части. Вычисляя левую часть равенства б) в формулировке леммы Лагранжа, получим:
 =
= 

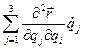 . (35)
. (35)
Последнее равенство в соотношении (35) записано на основе того, что функция 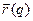 дважды непрерывно дифференцируема по переменным
дважды непрерывно дифференцируема по переменным  ,
,  ,
,  . А тогда смешанные производные от
. А тогда смешанные производные от  по
по 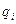 и
и 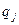 будут непрерывными и, следовательно, порядок дифференцирования при их вычислении можно переставлять. При такой перестановке значения смешанных производных будут совпадать:
будут непрерывными и, следовательно, порядок дифференцирования при их вычислении можно переставлять. При такой перестановке значения смешанных производных будут совпадать:
 =
= 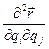 .
.
Сопоставляя (35) и (34), видим, что правая и левая части равенства б) совпадают. Лемма доказана.
Применим лемму Лагранжа к выводу формулы для вычисления ковариантных координат  ,
,  , скорости
, скорости 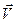 . Поскольку
. Поскольку
 =
=  ,
, 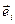 =
= 
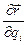 ,
,  ,
,
то можем записать
 =
= 
 =
= 
 .
.
Подставляя соотношение а) из леммы Лагранжа и учитывая, что 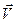 задается формулой (31), а для нее справедливо очевидное равенство
задается формулой (31), а для нее справедливо очевидное равенство
 =
= 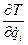 ,
,
где 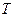 =
= 
 =
=  , окончательно находим
, окончательно находим
 =
= 
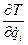 ,
,  . (36)
. (36)
Отметим здесь, что полученная формула (36) для  отличается по виду от (30). Однако легко видеть, что она совпадает с (30), если учесть в (36), что функция
отличается по виду от (30). Однако легко видеть, что она совпадает с (30), если учесть в (36), что функция 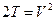 задается правой частью равенства (29). На практике часто бывает удобнее сначала построить функцию
задается правой частью равенства (29). На практике часто бывает удобнее сначала построить функцию 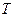 , а затем для вычисления
, а затем для вычисления  применить формулу (36) вместо непосредственного применения (30).
применить формулу (36) вместо непосредственного применения (30).
В заключение установим связь декартовых и криволинейных координат скорости. Легко видеть, что
 =
=  =
=  =
=  =
=  =
=  .
.
Отсюда круговой перестановкой координат  и ортов
и ортов 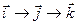 получим выражения для
получим выражения для  и
и  :
:
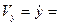
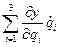


 ,
,




 .
.
В матричной записи полученные выражения для  ,
,  и
и  примут вид:
примут вид:
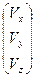 =
=  =
=  ,
,
где  — матрица перехода от аффинной системы к декартовой прямоугольной системе координат,
— матрица перехода от аффинной системы к декартовой прямоугольной системе координат,
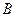 =
=  .
.
В данном выражении элементы матрицы 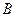 вычисляются в точке
вычисляются в точке  (а не в точке
(а не в точке 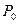 ).
).
Дата добавления: 2015-04-15; просмотров: 251; Мы поможем в написании вашей работы!; Нарушение авторских прав |