
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение 10.
Величина  называется обобщенной скоростью точки
называется обобщенной скоростью точки  по координате
по координате 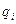 в момент времени
в момент времени  . Величина
. Величина 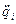 называется обобщенным ускорением точки
называется обобщенным ускорением точки  по координате
по координате 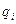 в момент времени
в момент времени  .
.
Установим формулу связи скорости 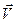 и ее контравариантных координат
и ее контравариантных координат  с обобщенными скоростями
с обобщенными скоростями  в произвольный момент времени
в произвольный момент времени  . Поскольку в векторной форме движение задается формулой
. Поскольку в векторной форме движение задается формулой
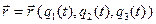 ,
,
то по определению скорости 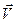 можем записать
можем записать
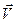 =
= 
 .
.
С одной стороны, вычисляя производную с учетом того, что функция, стоящая под символом  , является суперпозицией вектор-функции
, является суперпозицией вектор-функции 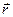 от трех переменных
от трех переменных  ,
,  ,
,  и заданных функций
и заданных функций 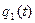 ,
,  ,
,  , зависящих от времени
, зависящих от времени  , будем иметь
, будем иметь
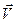 =
=  =
= 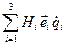 . (26)
. (26)
С другой стороны, вектор 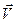 можем разложить по базису
можем разложить по базису 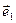 ,
,  ,
,  , вычисленному в точке
, вычисленному в точке  , имеющей значения криволинейных координат
, имеющей значения криволинейных координат  =
= 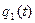 ,
,  =
=  ,
,  =
=  в заданный момент времени
в заданный момент времени  . И тогда придем к следующему выражению для
. И тогда придем к следующему выражению для 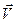 :
:
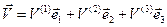 . (27)
. (27)
Согласно определению координат любого вектора, множители  при базисных векторах
при базисных векторах 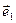 ,
,  ,
,  в разложении (27) называются контравариантными координатами скорости
в разложении (27) называются контравариантными координатами скорости 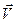 в аффинной системе, имеющей начало в точке
в аффинной системе, имеющей начало в точке  .
.
Сопоставляя (26) и (27), получаем
 =
=  ,
,  . (28)
. (28)
Здесь  — коэффициент Ламе по координате
— коэффициент Ламе по координате 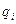 , соответствующий моменту времени
, соответствующий моменту времени  .
.
Формула (28) дает связь контравариантных координат скорости 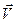 с обобщенными скоростями
с обобщенными скоростями  ,
,  .
.
С учетом (27) и (28), находим выражение для квадрата модуля скорости:



 . (29)
. (29)
Установим теперь связь ковариантных координат  ,
,  , с обобщенными скоростями
, с обобщенными скоростями  . Согласно определению ковариантной координаты имеем
. Согласно определению ковариантной координаты имеем 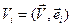 . Подставляя (27) и (28), находим искомую связь
. Подставляя (27) и (28), находим искомую связь
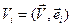

 . (30)
. (30)
В частности, из (28), (29) и (30) можем сделать следующий вывод.
Если  — ортогональный ортонормированный базис при любых значениях
— ортогональный ортонормированный базис при любых значениях  ,
,  ,
,  (т.е. криволинейные координаты
(т.е. криволинейные координаты  ,
,  ,
,  — ортогональные), то
— ортогональные), то
 =
=  ,
,  , и
, и  =
=  .
.
В общем случае (когда криволинейные координаты — не ортогональные) ковариантные и контравариантные координаты будут отличаться друг от друга:
 ¹
¹  ,
,  .
.
Дадим другой способ вычисления координат  . Для этого сначала введем в рассмотрение функцию
. Для этого сначала введем в рассмотрение функцию 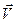 , зависящую от шести независимых переменных, и докажем лемму Лагранжа, устанавливающую связь производных от функции
, зависящую от шести независимых переменных, и докажем лемму Лагранжа, устанавливающую связь производных от функции 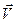 и от функции
и от функции  .
.
Указанную функцию 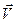 определим следующей формулой
определим следующей формулой
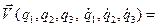
 . (31)
. (31)
Независимыми переменными в ней будем считать криволинейные координаты  ,
,  ,
,  и обобщенные скорости
и обобщенные скорости 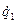 ,
,  ,
,  . Следует заметить, что точка, стоящая в обозначениях переменных
. Следует заметить, что точка, стоящая в обозначениях переменных 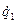 ,
,  ,
,  , не означает дифференцирование переменных
, не означает дифференцирование переменных  ,
,  ,
,  по времени
по времени  . Это всего лишь символ в данных обозначениях.
. Это всего лишь символ в данных обозначениях.
В правой части равенства (31) вектор 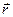 является вектор-функцией
является вектор-функцией  , задающей связь (1) криволинейных координат точки с декартовыми.
, задающей связь (1) криволинейных координат точки с декартовыми.
Функцию  будем считать заданной при всех
будем считать заданной при всех  и при любых значениях
и при любых значениях 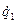 ,
,  ,
,  .
.
Поскольку  дважды непрерывно дифференцируема по своим аргументам, то
дважды непрерывно дифференцируема по своим аргументам, то  будет непрерывно дифференцируема по переменным
будет непрерывно дифференцируема по переменным  ,
,  ,
,  . Кроме того, она линейна по обобщенным скоростям
. Кроме того, она линейна по обобщенным скоростям 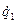 ,
,  ,
,  .
.
Пусть задано произвольное движение точки  в криволинейных координатах
в криволинейных координатах  ,
,  . Вычислим значения функции
. Вычислим значения функции  на этом движении, полагая, что переменные
на этом движении, полагая, что переменные  ,
,  , связаны с обобщенными скоростями
, связаны с обобщенными скоростями  в любой момент времени
в любой момент времени  на данном движении равенствами
на данном движении равенствами
 ,
,  .
.
Для того чтобы вычислить искомое значение функции, необходимо заменить в правой части равенства (31) переменные 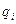 на
на  , а
, а  — на
— на  ,
,  .
.
Действительно, согласно определению мгновенной скорости 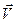 в момент времени
в момент времени  , необходимо вычислить движение
, необходимо вычислить движение  , а затем взять производную по
, а затем взять производную по  от него. Так что будем иметь
от него. Так что будем иметь


 .
.
Это выражение будет совпадать со значением функции 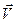 , задаваемым формулой (31), в котором переменные
, задаваемым формулой (31), в котором переменные 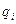 заменены на
заменены на  , а
, а  на
на  для
для  .
.
В результате получим вектор  , совпадающий по значению с вектором
, совпадающий по значению с вектором 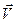 , вычисленным по формуле (26).
, вычисленным по формуле (26).
Поскольку установленное таким образом равенство справедливо на любом движении и в любой момент времени  , то можем сделать заключение о том, что формула (31) дает связь обобщенных скоростей точки с ее скоростью в абсолютном пространстве в соответствующем положении
, то можем сделать заключение о том, что формула (31) дает связь обобщенных скоростей точки с ее скоростью в абсолютном пространстве в соответствующем положении
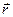 =
=  .
.
Установим теперь связь производных 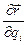 от функции
от функции  с производными
с производными  и
и  от функции
от функции  . Такая связь дается леммой Лагранжа. Прежде чем формулировать лемму Лагранжа, введем понятие производной от функции
. Такая связь дается леммой Лагранжа. Прежде чем формулировать лемму Лагранжа, введем понятие производной от функции 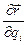 вдоль движений точки
вдоль движений точки  .
.
Вычислим производную 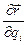 от функции
от функции  и обозначим ее
и обозначим ее 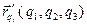 . Пусть задано движение точки
. Пусть задано движение точки  в криволинейных координатах
в криволинейных координатах
 ,
, 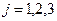 . (32)
. (32)
Определим значения функции 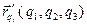 , которые она может принимать на движении (32). Ясно, что эти значения задаются вектор-функцией
, которые она может принимать на движении (32). Ясно, что эти значения задаются вектор-функцией  , которая получается заменой в
, которая получается заменой в 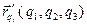 аргументов
аргументов 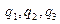 на правые части (32).
на правые части (32).
Вычислим производную по 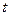 от функции
от функции  .
.
 . (33)
. (33)
Функция  , стоящая в левой части (33), имеет смысл скорости изменения функции
, стоящая в левой части (33), имеет смысл скорости изменения функции 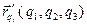 вдоль движения (32). В правой части (33) указывается ее аналитический вид, построенный по правилам дифференцирования по времени
вдоль движения (32). В правой части (33) указывается ее аналитический вид, построенный по правилам дифференцирования по времени  функции
функции 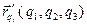 как сложной функции, в которой аргументы
как сложной функции, в которой аргументы 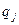 ,
, 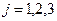 , задаются движением (32).
, задаются движением (32).
Как известно, правило дифференцирования сложной функции предполагает выполнение следующих операций.
1. Вычисление частных производных от функции 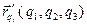 . В результате получают три функции,
. В результате получают три функции,
 ,
, 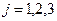 ,
,
зависящие от трех переменных 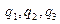 .
.
2. Каждая функция  с номером
с номером  умножается на переменную
умножается на переменную  , и производится суммирование по
, и производится суммирование по 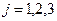 всех построенных произведений. В результате будет построена функция, зависящая от шести переменных
всех построенных произведений. В результате будет построена функция, зависящая от шести переменных 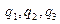 и
и 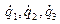 . Будем записывать эту функцию в операторной форме
. Будем записывать эту функцию в операторной форме  или, что то же самое, в форме
или, что то же самое, в форме 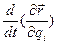 . В явном выражении этот оператор принимает вид:
. В явном выражении этот оператор принимает вид:
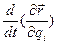
 . (34)
. (34)
3. В построенной на этапе 2 функции (34) переменные 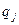 заменяются функциями
заменяются функциями  , а переменные
, а переменные  — производными
— производными 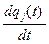 ,
, 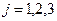 , где
, где  — правые части (32), определяющие заданное движение материальной точки.
— правые части (32), определяющие заданное движение материальной точки.
Результатом произведенных действий, описанных на этапах 1,2,3, является функция, зависящая только от одной независимой переменной — от времени 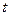 , которая совпадает с правой частью равенства (33).
, которая совпадает с правой частью равенства (33).
Однако обратимся к функции (34), построенной в процессе вычислений на этапе 2.
Дата добавления: 2015-04-15; просмотров: 221; Мы поможем в написании вашей работы!; Нарушение авторских прав |