
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение 6.
Если основная система координат ортогональна при любых значениях 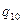 ,
, 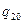 ,
, 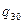 из области
из области 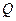 , то криволинейные координаты
, то криволинейные координаты  ,
,  ,
,  называются ортогональными.
называются ортогональными.
Справедливо следующее утверждение.
Криволинейные координаты ортогональны тогда и только тогда, когда при любых 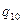 ,
, 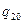 ,
, 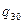 из области
из области 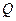 выполняются условия
выполняются условия
 ,
, 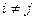 ,
, 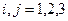 . (9)
. (9)
Утверждение очевидно.
Следует отметить, что условия (9) ортогональности криволинейных координат должны выполняться при любых значениях криволинейных координат 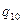 ,
, 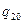 ,
, 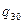 из области
из области 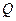 . Иначе говоря, равенства (9) должны быть справедливы в любом положении точки
. Иначе говоря, равенства (9) должны быть справедливы в любом положении точки 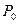 . Этот вывод вытекает из определения 6 ортогональных криволинейных координат.
. Этот вывод вытекает из определения 6 ортогональных криволинейных координат.
Но данное требование равносильно тому, что соотношения (9) должны выполняться в любой точке  , имеющей координаты
, имеющей координаты  .
.
Поэтому при вычислении векторов  и
и 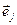 по формулам (5) можно заменить в (5) координаты
по формулам (5) можно заменить в (5) координаты 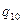 ,
, 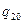 ,
, 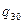 точки
точки 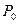 на координаты
на координаты  ,
,  ,
,  точки
точки  .
.
Такое действие позволяет исключить индекс «0» в обозначении аргументов 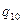 ,
, 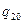 ,
, 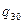 при вычислении производных от вектор-функции
при вычислении производных от вектор-функции  в формулах (6) и требовать от равенств (9), чтобы они выполнялись при любых значениях
в формулах (6) и требовать от равенств (9), чтобы они выполнялись при любых значениях  .
.
С учетом сказанного условия (9) в скалярной форме примут вид:

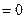 ,
, 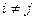 ,
, 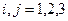 , при
, при  .
.
К ним следует присоединить условие (2) некомпланарности векторов 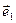 ,
,  ,
,  :
:
 ,
,
причем:
– если тройка векторов 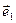 ,
,  ,
,  правая, то
правая, то


 ,
, 
 ,
, 
 ,
,
– если тройка векторов 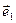 ,
,  ,
,  левая, то
левая, то


 ,
, 
 ,
, 
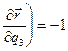 .
.
Дата добавления: 2015-04-15; просмотров: 209; Мы поможем в написании вашей работы!; Нарушение авторских прав |