Замечания. 1. На практике иногда удается указать переменные , , , которые удовлетворяют описанным условиям не для любой точки

1. На практике иногда удается указать переменные , , , которые удовлетворяют описанным условиям не для любой точки абсолютного пространства, а лишь для некоторого множества из него. Если по предварительным прогнозам из каких-либо соображений известно, что на изучаемых моделях движения материальная точка не покинет указанное множество, то переменные , , могут быть приняты за обобщенные координаты для описания и исследования таких движений.

2. Если отсутствуют криволинейные координаты , , , для которых справедливы сформулированные выше свойства во всем абсолютном пространстве, то можно вводить криволинейные координаты , , для части пространства, в которой эти условия выполняются.

Для оставшейся части пространства можно подобрать другие переме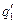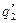нные , , так, чтобы для них выполнялись указанные условия. Причем новые переменные 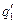, , 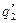вводятся так, чтобы не нарушались условия из определения криволинейных координат и в некоторой части пространства, где они справедливы и для переменных , , .

Общая часть пространства для переменных , , и 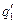, , 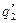позволяет при изучении движений осуществлять переход от криволинейных координат , , к криволинейным координатам 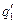, , 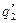, как только материальная точка окажется в этой общей части пространства.

Пример 1. Цилиндрическая система координат.

( )

( )

( )

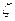
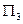
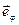
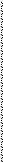
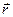
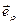
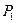
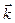
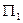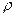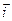
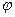
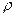
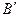
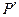
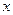Рис. 1.

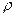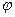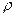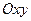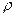
Положение точки задается переменными , , (см. рис.1), где — расстояние от полюса до проекции точки на плоскость ; ; 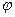— угол в плоскости 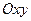, отсчитываемый от положительного направления оси 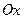до луча ( 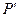— это проекция точки на плоскость 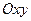); ; положительное направление отсчета угла 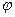задается правилом правой руки; 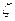— проекция радиус-вектора 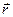точки на ось ; ( , — проекция точки на ось ); .

Связь декартовых прямоугольных координат 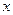, , точки с цилиндрическими задается следующими формулами:

= , = , = .

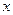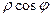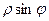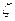Обратная зависимость 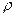, , 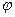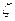от 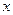, , , т.е. связь цилиндрических координат с декартовыми, имеет вид:

= , , = .

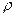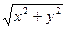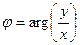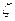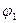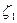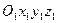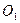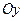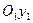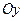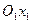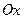Если , то аналогичным образом можно ввести цилиндрические координаты , , по отношению к системе координат , у которой, например, полюс смещен вдоль оси , ось совпадает с осью , а оси и коллинеарны осям и .

В тех случаях, когда движения точки могут приводить ее на ось , следует переходить к описанию этих движений в переменных , , .

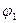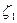Пример 2. Сферическая система координат.

Положение точки задается криволинейными координатами 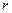, , 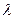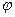(см. рис.2). Они имеют следующий геометрический смысл.

Координата 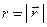обозначает расстояние от полюса декартовой прямоугольной системы координат до точки . Она может принимать значения .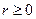

Координата 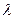обозначает угол в плоскости 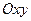, отсчитываемый от положительного направления оси 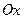до проекции вектора на плоскость 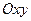. Она может изменяться в диапазоне 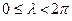. Положительное направление отсчета угла 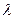задается правилом правой руки относительно орта .

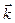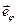
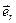
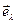
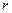
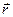
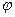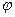
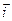
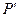
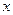Рис. 2.

Координата 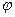определяется значением угла между плоскостью 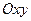и радиус-вектором точки . Угол 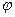отсчитывается от плоскости 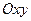до радиус-вектора и может изменяться в диапазоне 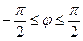. Он принимает значение 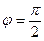, если точка находится на положительной полуоси ; , если находится на отрицательной полуоси , и 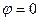, если находится в плоскости .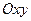

Угол 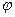положителен, если точка принадлежит положительному полупространству относительно плоскости 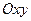; угол 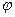отрицателен, если находится в отрицательном полупространстве 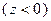относительно плоскости .

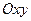На рисунке 2 точка 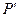обозначает ортогональную проекцию точки на плоскость 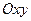, а — ортогональную проекцию точки на ось .

Связь декартовых прямоугольных координат 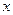, , точки со сферическими задается формулами:

, , .

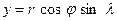Обратная зависимость, т.е. связь сферических координат с декартовыми, имеет вид:

, , .

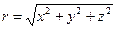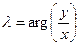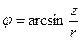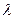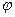Угол не определен, если точка находится на оси . Угол не определен, если точка совпадает с точкой отсчета .