Ordm;. Союзная система координат и ее связь с основной.

Ковариантные координаты вектора.

Пусть — произвольный вектор; 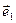, , — базис основной системы координат; 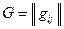, 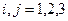— матрица метрических коэффициентов этой системы, ; , , 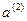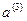— координаты вектора в основной системе. Как отмечено выше, они называются контравариантными координатами вектора . Введем следующее понятие.

Определение 8.

Ковариантнымикоординатами вектора называются величины , определяемые по формуле:

, .

Геометрический смысл ковариантных координат вектора следующий:

— если вектора 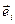, , являются ортами, то — это ортогональные проекции вектора на координатные оси основной системы координат,

— если вектора 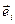, , не являются ортами, то — это ортогональные проекции вектора на указанные оси, умноженные на , где = .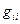

Введем следующие три вектора , , :

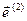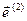
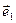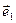
( ), ( ), ( ) (15)

и изучим их свойства. В (15) буквой обозначена величина смешанного произведения векторов , , :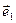

. (16)

Как показано в п.5º, в этих обозначениях будем иметь .