Определение 11.

Функция, определяемая правой частью (34), называется производной от функции 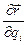вдоль движений механической системы и обозначается .

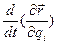В отличие от функции (33), функция (34) зависит от шести переменных 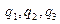и 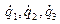. Из ее построения следует, что подстановкой в нее вместо 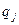любого фиксированного движения материальной точки, заданного в криволинейных координатах, и подстановкой в нее вместо — обобщенных скоростей на данном фиксированном движении, будет определена скорость изменения функции 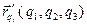вдоль этого движения. Иначе говоря, зная функцию (34), можно определить скорость изменения функции 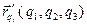на любом заданном движении, а не только на движении (32). Поэтому функция (34) играет в дальнейшем важную роль.

Отметим, что функция, стоящая в правой части равенства (34), получена на основе действий, описанных в первых двух этапах вычисления производной по времени 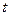от функции 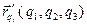. В таких случаях говорят, что «она получена дифференцированием функции 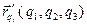вдоль движений (на движениях) материальной точки». Применительно к ее обозначению 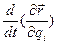, записанному в левой части (34), также говорят, что «в левой части равенства (34) дифференцирование функции 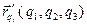по времени 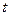производится вдоль движений материальной точки». В указанных случаях результат дифференцирования, т.е. правая часть равенства (34), задающая явный вид построенной функции, как правило, не приводится.

Докажем теперь следующую лемму Лагранжа.