
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Лагранжа.
Вычислим ускорение точки 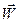 согласно определению
согласно определению 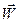 =
=  . Учтем, что
. Учтем, что 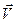 =
=  =
=  .
.
Дифференцируя правую часть по  , приходим к векторному представлению ускорения
, приходим к векторному представлению ускорения 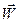 в зависимости от вектор-функции
в зависимости от вектор-функции  , обобщенных скоростей
, обобщенных скоростей  и обобщенных ускорений
и обобщенных ускорений  ,
,  :
:
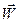 =
=  =
=  +
+  .
.
В проекциях на абсолютные оси 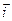 ,
,  ,
, 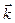 оно примет вид:
оно примет вид:
 =
=  =
=  +
+  ,
,  =
=  =
=  +
+  ,
,
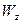 =
=  =
=  +
+  .
.
Запишем теперь разложение ускорения 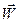 по базису
по базису 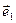 ,
,  ,
,  основной системы с началом в точке
основной системы с началом в точке  и по базису
и по базису 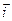 ,
,  ,
, 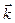 ДПСК:
ДПСК:
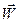 =
=  =
= 
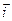 +
+ 
 +
+ 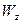
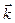 . (37)
. (37)
Умножая обе части равенства последовательно на 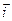 ,
,  ,
, 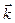 скалярно, находим:
скалярно, находим:
 =
=  (
( 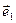 ,
, 
 (
(  ,
, 
 (
(  ,
, 
 ,
,
 =
=  (
( 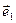 ,
, 
 (
(  ,
, 
 (
(  ,
, 
 ,
,
 =
=  (
( 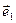 ,
, 
 (
(  ,
, 
 (
(  ,
, 
 .
.
В матричном представлении данные соотношения примут вид:
 =
= 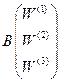 , или
, или 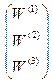 =
= 
 .
.
Они дают связь контравариантных координат  ,
,  ,
,  ускорения
ускорения 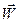 с его декартовыми координатами
с его декартовыми координатами  ,
,  ,
,  . Из равенства
. Из равенства  подстановкой в него разложения (37) получаем формулу для
подстановкой в него разложения (37) получаем формулу для  :
:
 =
=  ,
,
где  — модуль ускорения
— модуль ускорения 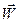 .
.
Построим теперь формулу Лагранжа для вычисления ковариантных координат  ,
,  , ускорения
, ускорения 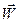 . Согласно определению ковариантных координат можем записать
. Согласно определению ковариантных координат можем записать  =
=  ,
,  . Подставим в правую часть этого равенства значение орта
. Подставим в правую часть этого равенства значение орта 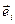 , вычисленное в точке
, вычисленное в точке  ,
,
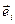 =
= 
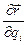
и вынесем 
 за знак скалярного произведения. В результате придем к следующему выражению для
за знак скалярного произведения. В результате придем к следующему выражению для  :
:
 =
=  (
(  ,
, 




 .
.
В нем, в соответствии с определением понятия ускорения точки, производная  вычисляется вдоль движения
вычисляется вдоль движения  =
= 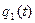 ,
,  =
=  ,
,  =
=  . Поэтому в множителе
. Поэтому в множителе  производная по времени строится от суперпозиции функций
производная по времени строится от суперпозиции функций 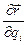 и
и 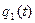 ,
,  ,
,  .
.
А потому, согласно свойству б) функции  из леммы Лагранжа, множитель
из леммы Лагранжа, множитель  можно заменить производной
можно заменить производной  . Кроме того, по свойству а) из той же леммы, множитель
. Кроме того, по свойству а) из той же леммы, множитель 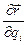 можно заменить производной
можно заменить производной  . А тогда выражение для
. А тогда выражение для  примет вид
примет вид
 =
= 




 . (38)
. (38)
Введем функцию  , где
, где 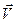 задается формулой (31). Будем иметь
задается формулой (31). Будем иметь


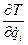 ,
, 

 .
.
Подставляя в (38), окончательно найдем
 =
= 

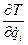
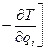 ,
,  . (39)
. (39)
Эта формуланазывается формулойЛагранжа для вычисления ковариантных координат ускорения точки. Таким образом, доказали следующую теорему.
Теорема Лагранжа.
Ковариантные координаты вектора 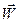 ускорения материальной точки выражаются по формуле(39).
ускорения материальной точки выражаются по формуле(39).
Если криволинейные координаты ортогональны, то  =
=  ,
,  . В таком случае формула (38) позволяет вычислить контравариантные координаты
. В таком случае формула (38) позволяет вычислить контравариантные координаты  вектора
вектора 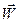 .
.
Дата добавления: 2015-04-15; просмотров: 233; Мы поможем в написании вашей работы!; Нарушение авторских прав |