Ordm;. Связь между составляющими движениями в сложном движении материальной точки.

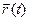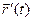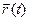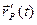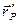
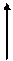
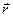
Найдем связь между абсолютным, переносным и относительным движением материальной точки. Для этого сначала рассмотрим абсолютное движение материальной точки . Будем определять его через движение , задаваемое относительно точки отсчета . Пусть точка в момент времени занимает положение = . Положение точки в этот же момент времени относительно точки отсчета обозначим (см. рис.2).

Рис.2.

Если 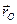= 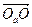— положение точки отсчета в момент относительно точки отсчета 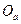, то по правилу сложения векторов можем записать

= + ,

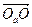или иначе

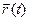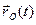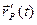= = + . (11)

В координатной форме это векторное соотношение примет вид:

= ,

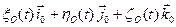
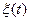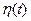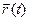где , , — координаты вектора ,

, , — координаты вектора ,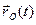

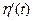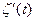, , — координаты вектора .

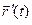Координаты всех векторов задаются в абсолютной системе координат.

Будем теперь рассматривать положение точки в этот же момент времени относительно точки отсчета в подвижном пространстве. Это положение задается вектор-функцией 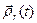, т.е. имеем

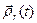= = . (12)

Вектор-функция 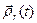определяет относительное движение точки . В координатной форме равенство (12) примет вид:

.

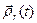Здесь , , 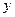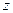— координаты точки в момент времени в подвижной

системе координат , или иначе, это координаты

вектора ;

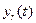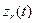, , — координатные функции относительного движения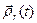

в подвижной системе координат .

Поскольку 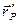= и = , то можем записать

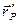= . (13)

Векторы 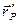и задаются в разных системах координат. В координатной форме равенство (13) выполняется в каждый момент времени и имеет вид:

.

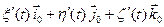
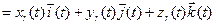Здесь 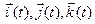— вектор-функции, задающие движение базиса подвижного пространства в абсолютном .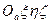

Если 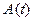— матрица ориентации пространства относительно пространства 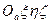в момент времени , то можем записать

= ,

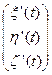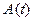
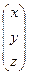или иначе,

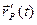= . (14)

Поэтому, подставляя (14) в (11), получим

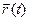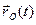= + , (15)

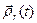
где = 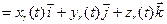. (16)

В (15) слева стоит вектор-функция, определяющая абсолютное движение точки , а справа — функция, записанная в векторно-матричной форме, задающая движение некоторого фиктивного твердого тела. Для него связанной системой координат служит подвижная система . В (15) условно следует считать вектор неподвижным в системе . Этот вектор совпадает с тем положением точки твердого тела, которое занимает в нем в момент времени точка .

В (16) слева стоит вектор , указывающий в момент времени положение точки в фиктивном твердом теле. Справа в (16) стоит вектор-функция 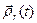, задающая относительное движение точки . Следовательно, равенство (15) означает, что абсолютное движение точки (левая часть равенства (15)) совпадает с движением той точки фиктивного твердого тела (правая часть равенства (15)), с которой в момент времени по положению совпадает материальная точка .

По определению 4 переносного движения точки векторная функция, стоящая справа в (15), — это функция, задающая переносное движение указанной точки (см. (10)).

Равенство (16) (по определению 1) — это относительное движение точки .

Таким образом, соотношения (15) и (16) устанавливают связь между абсолютным, переносным и относительным движением точки .

Подставляя (16) в (15), получим эту связь в виде одного равенства, записанного в векторно-матричной форме

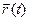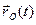
= . (17)

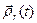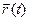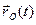В (17) задается координатными функциями в подвижных осях, а и – координатными функциями в абсолютных осях. Столбцы матрицы 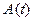содержат законы изменения направляющих косинусов базисных ортов подвижных осей в абсолютном пространстве.

Сопоставляя правые части (10) и (17), можем сделать следующее заключение, которое сформулируем в виде теоремы.

Теорема.

Абсолютное движение 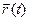точки является суперпозицией её переносного движения и относительного движения .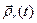

Это утверждение можно записать в виде равенства

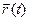= . (18)

Данная теорема называется теоремой связи абсолютного и составляющих движений в сложном движении точки.