Примечание. В дальнейшем слово «мгновенный» в названии векторов , , ,

В дальнейшем слово «мгновенный» в названии векторов 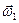, , , 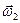будем опускать, если это не вызовет недоразумений.

Приступим теперь к решению первой задачи кинематики сложного движения твердого тела — установим связь между его абсолютным движением и составляющими движениями.

Очевидно, из правила сложения векторов имеем (см. рис.3)

= + + .

Подставляя принятые обозначения, получаем

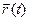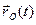= + + . (12)

Учитывая, что вектор имеет координаты , , в системе , можем записать

= + + .

Вектор задается координатами , , 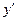в связанной системе

= ,

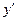, , — постоянные величины для каждой точки твердого тела.

Если представить правую часть равенства (12) в проекциях на абсолютные оси, то в векторно-матричной форме равенство (12) примет вид:

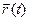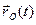= + + . (13)

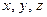Здесь под вектором понимается вектор , имеющий координаты в подвижной системе, вычисляемые по формуле

.

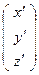Под вектором + понимается вектор . Он имеет координаты в абсолютной системе 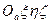, которые вычисляются по формуле

+ .

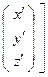Соотношение (13) задает связь абсолютного движения 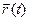любой точки твердого тела, имеющей координаты , , 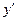в связанной системе , с составляющими движениями, задаваемыми вектор-функцией 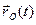и матрицей ориентации (это первое составляющее движение), вектор-функцией и матрицей ориентации твердого тела в подвижном пространстве (это второе составляющее движение).

Таким образом, формула (13) дает решение первой задачи кинематики сложного движения твердого тела.

Замечание 2.

Соотношение (13) может быть получено непосредственно из теоремы связи абсолютного движения и составляющих движений материальной точки, доказанной в §1, п.2º. Действительно, каждая точка твердого тела совершает сложное движение.В соответствии с указанной теоремой ее абсолютное движение 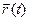связано с переносным и относительным 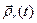по формуле (18) из §1, п.2º.

В задаче о сложном движении твердого тела переносное движение точки определяется функцией

= + .

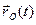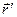Здесь 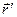= – положение точки в подвижном пространстве , которое при построении функции условно считается постоянным. Относительное движение точки описывается функцией

= = + ,

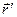определяемой из формулы задания движения твердого тела в подвижной системе координат . В ней = – положение точки в связанной системе 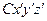. Оно является неизменным в этой системе.

Суперпозиция функций и 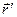= , задающих переносное и относительное движения точки , с одной стороны, приводит к соотношению (13). С другой стороны, согласно указанной теореме, она определяет связь абсолютного движения и составляющих движений точки .

Поскольку полученное соотношение (13) справедливо для любой точки твердого тела, то этим установлена связь абсолютного и составляющих движений твердого тела.