Ordm;. Теорема о сложении скоростей.

Теорема (о сложении скоростей).

Абсолютная скорость точки в сложном движении равна сумме переносной скорости точки и ее относительной скорости, т.е. справедливо равенство

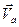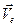= + . (12)

Доказательство.

Как показано в п.2º§1, положение 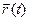точки в абсолютном пространстве в момент времени можем представить в виде суммы

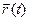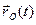= + , (13)

где 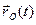— положение полюса подвижной системы

в абсолютном пространстве в момент времени ,

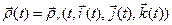— положение точки в момент времени

относительно полюса .

Вектор-функци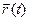и и 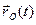задаются разложениями (1) и (4) из §1, соответственно. Вектор-функция определяется формулой (21) в §1. В ней векторы 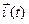, , 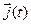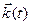задаются направляющими косинусами в абсолютной системе 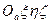элементами матрицы 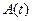. Поэтому проекции , , 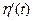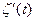вектора на оси абсолютной системы связаны с координатными функциями , , 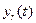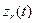и матрицей 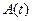следующими соотношениями

= ,

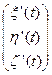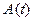
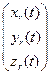Таким образом, имеем .

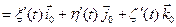Разложение вектора по подвижному базису , , в любой момент времени совпадает с разложением вектор-функция 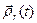, задающей относительное движение точки. Так что согласно (6) из §1 можем записать: = .

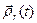
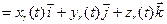Дифференцируем равенство (13) по :

= = + .

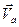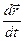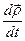Будем рассматривать здесь вектор как вектор-функцию, заданную в проекциях на подвижные оси. Тогда = 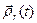. Применяя к вектору формулу (11), получим

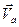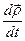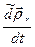
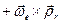= + = + . (14)

В правой части этого равенства имеем:

– в соответствии с определением 1 из §2, — это абсолютная скорость точки (полюса подвижной системы);

– в соответствии с определением 2 из §2, 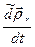= — относительная скорость точки ;

– согласно формуле (8), 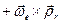= 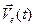— переносная скорость точки .

Заменяя в правой части (14) указанные выражения на и 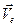, придем к равенству (12). Теорема доказана.