Теорема о сложении угловых скоростей.

Пусть 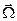- вектор мгновенной угловой скорости твердого тела относительно абсолютного пространства 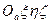. Тогда справедливо следующее утверждение.

Следствие 1.

Вектор 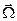мгновенной угловой скорости твердого тела относительно абсолютного пространства в сложном движении равен векторной сумме мгновенных угловых скоростей 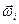, , составляющих движений:

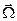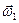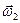= + . (18)

Утверждение следствия 1 легко распространяется на случай составляющих движений.

Следствие 2.

Если твердое тело участвует в составляющих движениях, то формула (18) имеет вид:

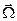= . (19)

Действительно, если равенство (18) будет доказано, то по индукции легко устанавливается справедливость формулы (19). Поэтому докажем равенство (18) (случай ).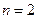

По формуле Эйлера абсолютная скорость 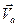любой точки твердого тела определяется через вектор 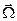следующим соотношением:

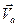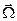
= + . (20)

С другой стороны, рассматривая движение твердого тела как сложное, имеющее два составляющих движения, согласно формуле (17) имеем

= + .

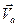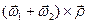Сопоставляя с (20), в силу произвольности получаем 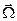= 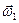+ 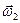, что и требовалось доказать.