
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формула для скоростей точек твердого тела в сложном движении.
Пусть  — произвольная точка твердого тела. Она участвует в сложном движении. Одно движение (переносное) — это движение подвижной системы
— произвольная точка твердого тела. Она участвует в сложном движении. Одно движение (переносное) — это движение подвижной системы  . Другое движение — относительное (это движение точки
. Другое движение — относительное (это движение точки  в подвижной системе
в подвижной системе  ).
).
Поэтому можем применить теорему о сложении скоростей:
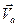 =
= 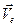 +
+  , (14)
, (14)
где 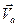 — абсолютная скорость,
— абсолютная скорость, 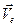 — переносная скорость,
— переносная скорость,  — относительная скорость точки
— относительная скорость точки  .
.
По определению переносной скорости можем записать
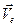 =
=  +
+ 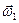

 +
+ 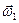

 +
+ 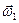

 .
.
Поскольку  +
+ 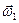

 =
=  — переносная скорость точки
— переносная скорость точки  , то переносная скорость
, то переносная скорость 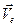 точки
точки  представляется в виде
представляется в виде
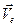 =
=  +
+ 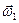

 . (15)
. (15)
По определению относительной скорости точки  согласно формуле Эйлера для скоростей точек твердого тела имеем
согласно формуле Эйлера для скоростей точек твердого тела имеем
 =
=  +
+ 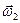

 , (16)
, (16)
где  — относительная скорость полюса связанной системы
— относительная скорость полюса связанной системы  (скорость точки
(скорость точки  относительно системы
относительно системы  ),
), 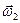

 — вращательная скорость точки
— вращательная скорость точки  относительно подвижной системы
относительно подвижной системы  .
.
Подставляя (15) и (16) в (14), придем к следующему выражению для скорости 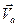 :
:
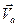 =
=  +
+ 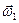

 +
+  +
+ 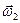

 =
=  +
+  +
+ 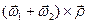 .
.
Поскольку  +
+  =
=  — абсолютная скорость точки
— абсолютная скорость точки  , то окончательно получим
, то окончательно получим
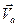 =
=  +
+ 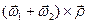 . (17)
. (17)
Таким образом, доказали теорему.
Теорема.
Абсолютная скорость любой точки  твердого тела равна сумме абсолютной скорости полюса
твердого тела равна сумме абсолютной скорости полюса  связанной с телом системы координат и векторного произведения суммы мгновенных угловых скоростей составляющих движений на радиус-вектор точки
связанной с телом системы координат и векторного произведения суммы мгновенных угловых скоростей составляющих движений на радиус-вектор точки  относительно полюса
относительно полюса  .
.
Дата добавления: 2015-04-15; просмотров: 239; Мы поможем в написании вашей работы!; Нарушение авторских прав |