
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ordm;. Постановка задачи о сложном движении твердого тела.
Будем говорить, что тело совершает сложное движение, если оно движется в пространстве, которое, в свою очередь, движется, т.е. является подвижным пространством.
Определение 1.
Движение твердого тела относительно подвижного пространства и движение подвижного пространства относительно абсолютного называются составляющими сложного движения твердого тела.
Замечание 1.
Подвижное пространство (в котором движется твердое тело) может совершать движение в другом подвижном пространстве, т.е. в пространстве, движущемся в абсолютном. Тогда также говорят, что это дополнительное подвижное пространство является составляющим движением сложного движения. Очевидно, в общем случае можем говорить, что твердое тело совершает сложное движение с  составляющими движениями.
составляющими движениями.
Основными задачами кинематики сложного движения является задача установления связи между абсолютным движением твердого тела и составляющими движениями, а также задача установления связи между кинематическими характеристиками составляющих движений и абсолютного движения твердого тела.
Будем рассматривать решение указанных задач в случае  . Результаты решения задач для
. Результаты решения задач для  легко распространяются на случай
легко распространяются на случай  .
.
Прежде чем приступить к решению поставленных задач, введем понятия мгновенной угловой скорости и мгновенного углового ускорения переносного и относительного движения твердого тела. Для этого сначала введем обозначения (см. рис.3):
– 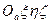 — абсолютная система координат с полюсом в точке
— абсолютная система координат с полюсом в точке 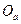 и базисом
и базисом  ,
,  ,
,  ;
;
–  — подвижная система координат с полюсом в точке
— подвижная система координат с полюсом в точке  и базисом
и базисом  ,
,  ,
,  ;
;
–  — связанная с твердым телом система координат с полюсом в точке
— связанная с твердым телом система координат с полюсом в точке  и базисом
и базисом  ,
,  ,
,  ;
;
–  — матрица ориентации подвижной системы
— матрица ориентации подвижной системы  в абсолютном пространстве, иначе, матрица перехода от
в абсолютном пространстве, иначе, матрица перехода от  к
к 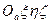 ;
;  ,
,  ;
;
–  — матрица ориентации твердого тела в подвижном пространстве
— матрица ориентации твердого тела в подвижном пространстве  , иначе, матрица перехода от
, иначе, матрица перехода от  к
к  ;
;  ,
,  .
.





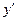
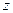



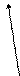


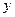









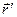



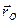

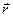

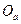

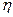
 Рис.3.
Рис.3.
Пусть  — произвольно выбранная точка твердого тела. Введем обозначения для следующих векторов:
— произвольно выбранная точка твердого тела. Введем обозначения для следующих векторов:
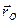 =
=  ,
,  =
=  ,
,  =
=  ,
,  =
=  ,
,  =
=  ,
, 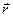 =
=  .
.
Здесь
– 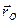 — положение полюса
— положение полюса  подвижной системы
подвижной системы  относительно точки отсчета
относительно точки отсчета 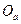 , выбранной в абсолютном пространстве; оно задается абсолютными координатами
, выбранной в абсолютном пространстве; оно задается абсолютными координатами 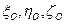 ;
;
–  — положение полюса
— положение полюса  связанной с твердым телом системы координат относительно точки отсчета
связанной с твердым телом системы координат относительно точки отсчета 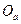 ; задается абсолютными координатами
; задается абсолютными координатами  ;
;
–  — положение полюса
— положение полюса  связанной системы относительно полюса
связанной системы относительно полюса  подвижной системы
подвижной системы  ; задается координатами
; задается координатами  в подвижной системе
в подвижной системе  ;
;
–  — положение точки
— положение точки  твердого тела в связанной системе
твердого тела в связанной системе  ; задается координатами
; задается координатами  ;
;
–  — положение точки
— положение точки  твердого тела в подвижном пространстве
твердого тела в подвижном пространстве  ; задается координатами
; задается координатами 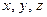 ;
;
– 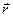 — положение точки
— положение точки  твердого тела относительно точки отсчета
твердого тела относительно точки отсчета 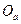 в абсолютном пространстве; задается абсолютными координатами
в абсолютном пространстве; задается абсолютными координатами  .
.
Теперь дадим понятия векторов мгновенной угловой скорости и мгновенного углового ускорения твердого тела в его переносном и относительном движениях.
Определение 2.
Переносной мгновенной угловой скоростью 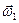 и переносным мгновенным угловым ускорением
и переносным мгновенным угловым ускорением  твердого тела в его сложном движении называются соответственно вектор мгновенной угловой скорости и вектор мгновенного углового ускорения подвижной системы координат
твердого тела в его сложном движении называются соответственно вектор мгновенной угловой скорости и вектор мгновенного углового ускорения подвижной системы координат  относительно абсолютного пространства.
относительно абсолютного пространства.
Сопоставляя данное определение 2 с определением 4 из §2 для векторов  и
и  , видим, что
, видим, что
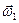 =
=  и
и  =
=  .
.
Как и вектор  , вектор
, вектор 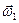 связан с движением базиса
связан с движением базиса  ,
,  ,
,  системы
системы  в абсолютном пространстве в любой момент времени
в абсолютном пространстве в любой момент времени  соотношением (5) §2.
соотношением (5) §2.
 . (1)
. (1)
В (1) вектор-функции  ,
,  ,
,  задаются своими проекциями на оси абсолютной системы координат, которые совпадают в каждый момент
задаются своими проекциями на оси абсолютной системы координат, которые совпадают в каждый момент  с элементами матрицы
с элементами матрицы  соответственно: проекции вектор-функции
соответственно: проекции вектор-функции  совпадают с элементами первого столбца,
совпадают с элементами первого столбца, 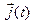 — второго,
— второго, 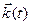 — третьего столбца. Поэтому можем записать
— третьего столбца. Поэтому можем записать
 ,
,

 , (2)
, (2)

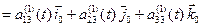 .
.
Разложения векторов  ,
,  ,
,  по базису
по базису  ,
,  ,
,  получаются дифференцированием по
получаются дифференцированием по  соотношений (2)
соотношений (2)

 ,
,

 , (3)
, (3)

 .
.
Из них следует, что координаты векторов  ,
,  ,
,  в абсолютной системе в момент времени
в абсолютной системе в момент времени  совпадают с элементами соответствующих столбцов матрицы
совпадают с элементами соответствующих столбцов матрицы  : координаты
: координаты  — с первым столбцом,
— с первым столбцом,  — со вторым,
— со вторым,  — с третьим столбцом.
— с третьим столбцом.
Вектор  определяется либо дифференцированием вектора
определяется либо дифференцированием вектора 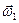 , т.е.
, т.е.  =
=  , либо по формуле
, либо по формуле
 . (4)
. (4)
В ней разложение векторов  ,
,  ,
,  по базису
по базису  ,
,  ,
,  в любой момент времени
в любой момент времени  получается дифференцированием по
получается дифференцированием по  соотношений (3). Таким образом, будем иметь
соотношений (3). Таким образом, будем иметь

 ,
,

 , (5)
, (5)

 .
.
Определение 3.
Вектором мгновенной угловой скорости 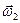 и вектором мгновенного углового ускорения
и вектором мгновенного углового ускорения  относительного движения твердого тела называются, соответственно, вектор мгновенной угловой скорости и вектор мгновенного углового ускорения твердого тела при его движении относительно подвижной системы координат
относительного движения твердого тела называются, соответственно, вектор мгновенной угловой скорости и вектор мгновенного углового ускорения твердого тела при его движении относительно подвижной системы координат  , условно принимаемой неподвижной.
, условно принимаемой неподвижной.
Из данного определения следует, что
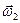 =
=  , (6)
, (6)
 . (7)
. (7)
Здесь  и
и  означают условные производные первого и второго порядка от вектор-функций
означают условные производные первого и второго порядка от вектор-функций  , заданных своими проекциями на оси подвижной системы
, заданных своими проекциями на оси подвижной системы  через элементы матрицы
через элементы матрицы  ориентации твердого тела в подвижном пространстве. При таком дифференцировании базис
ориентации твердого тела в подвижном пространстве. При таком дифференцировании базис  ,
,  ,
,  системы
системы  условно принимается неподвижным.
условно принимается неподвижным.
Легко заметить, что выражения (6) и (7) для векторов 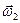 и
и  получаются из формул (1) и (4) путем замены в правых частях равенств (1) и (4):
получаются из формул (1) и (4) путем замены в правых частях равенств (1) и (4):
– подвижного базиса  ,
,  ,
,  переносного движения на базис связанной системы координат
переносного движения на базис связанной системы координат  ;
;
– дифференцирования 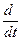 в абсолютной системе на условное дифференцирование
в абсолютной системе на условное дифференцирование  .
.
Поскольку векторы  ,
,  ,
,  в проекциях на базис
в проекциях на базис  ,
,  ,
,  «условно неподвижной» системы координат
«условно неподвижной» системы координат  в момент времени
в момент времени  задаются элементами соответствующих столбцов матрицы
задаются элементами соответствующих столбцов матрицы  перехода от связанной системы к системе
перехода от связанной системы к системе  , то можем записать
, то можем записать
 ,
,

 , (8)
, (8)

 .
.
В (8) векторы  ,
,  ,
,  , вообще говоря, зависят от
, вообще говоря, зависят от  . Однако в определении относительного движения твердого тела зависимость их от времени не учитывается. Движение твердого тела по отношению к системе отсчета
. Однако в определении относительного движения твердого тела зависимость их от времени не учитывается. Движение твердого тела по отношению к системе отсчета  является его движением в пространстве
является его движением в пространстве  , условно принятом за абсолютное пространство.
, условно принятом за абсолютное пространство.
Тем самым относительное движение тела определяется относительным движением полюса его связанной системы и движением базиса  этой системы относительно базиса
этой системы относительно базиса  ,
,  ,
,  , условно принятого неподвижным.
, условно принятого неподвижным.
Разложения векторов  ,
,  ,
,  по базису
по базису  ,
,  ,
,  получаются дифференцированием по
получаются дифференцированием по  соотношений (8), причем дифференцируются только направляющие косинусы
соотношений (8), причем дифференцируются только направляющие косинусы  ,
,  , а базис
, а базис  ,
,  ,
,  не дифференцируется:
не дифференцируется:

 ,
,

 , (9)
, (9)

 .
.
Аналогичным дифференцированием соотношений (9) строятся разложения векторов

 ,
,

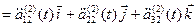 ,
,

 .
.
Очевидно, для векторов 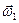 и
и 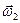 в любой момент времени
в любой момент времени  справедливы формулы Эйлера-Пуассона
справедливы формулы Эйлера-Пуассона
 =
= 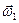

 ,
,  =
= 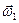

 ,
, 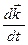 =
= 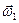

 . (10)
. (10)
 =
= 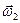

 ,
,  =
= 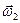

 ,
,  =
= 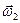

 . (11)
. (11)
Соотношения (10) следуют из определения вектора мгновенной угловой скорости подвижной системы координат  относительно абсолютного пространства
относительно абсолютного пространства 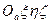 (см. определение 4 в §2).
(см. определение 4 в §2).
Формулы (11) вытекают из определения относительной производной от векторов  ,
,  ,
,  , заданных своими проекциями на оси подвижной системы
, заданных своими проекциями на оси подвижной системы  , и из определения 3 вектора мгновенной угловой скорости относительно системы
, и из определения 3 вектора мгновенной угловой скорости относительно системы  (условно принятой неподвижной).
(условно принятой неподвижной).
Дата добавления: 2015-04-15; просмотров: 264; Мы поможем в написании вашей работы!; Нарушение авторских прав |