Материальной точки.

Определение 1.

Абсолютной скоростью точки называется вектор

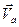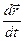= = . (1)

Абсолютным ускорением точки называется вектор

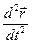= = = . (2)

Определение 2.

Относительной скоростью точки называется вектор

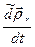
= . (3)

Относительным ускорением точки называется вектор

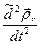= = = . (4)

В (3) и (4) обозначает относительную производную вектора, заданного своими координатами в подвижных осях (производная вектора, заданного проекциями на подвижные оси). По определению такой производной (условной производной) осуществляется дифференцирование по времени только координат вектора, а базисные векторы, хотя они и меняются по времени, не дифференцируются.

Определение 3.

Переносной скоростью 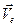и переносным ускорением точки в момент времени называются абсолютные скорость и ускорение точки фиктивного твердого тела, положение которой в этот момент совпадает с положением точки .

Определение 4.

Переносной мгновенной угловой скоростью и переносным мгновенным угловым ускорением называются мгновенная угловая скорость и мгновенное угловое ускорение подвижной системы координат относительно абсолютного пространства.

Из определения 4 и определения вектора мгновенной угловой скорости подвижной системы координат (см. гл.3, §8) следует

= . (5)

Вектор является решением уравнений Эйлера-Пуассона

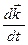= , = , = , (6)

в которых вектора , , , , , 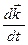вычисляются на заданном движении базиса системы в фиксированный момент времени .

Вектор мгновенного углового ускорения переносного движения связан с зависимостью

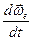= . (7)