Замечание.

Формулу (17) можно записать в векторном представлении

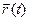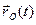
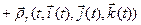= . (19)

В правой части равенства (19) стоит функция

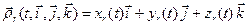, (20)

по виду совпадающая с вектор-функцией 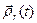, задающей относительное движение точки при любом фиксированном положении базиса , , подвижной системы координат. Значение вектор-функции (20) зависит не только от времени , но и от ориентации базиса , , в абсолютном пространстве.

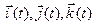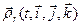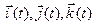Вектор-функции , выступающие в качестве аргументов в функции в правой части (19) суть функции, определяющие движение базиса системы . Это движение является вращением фиктивного твердого тела вокруг полюса . Проекции векторов на абсолютные оси в момент времени совпадают, соответственно, с элементами первого, второго и третьего столбцов матрицы .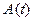

Если подставим функции 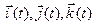в правую часть (20), то получим функцию следующего вида:

. (21)

Тогда равенство (19) с учетом (21) можно записать так:

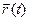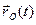= + . (22)

В нем вектор-функция определяется по формуле (21) и задает положение точки в любой момент времени относительно полюса в том случае, когда подвижная система координат совершает вращение вокруг полюса по закону

. (23)

По построению, функция — это суперпозиция функции (20), задающей относительное движение точки , и функций (23), задающих переносное движение подвижного пространства.

Переносным движением, соответствующим заданию (23), как отмечено выше, является вращение подвижного пространства вокруг фиксированной в нем точки отсчета и «условно» неподвижной в абсолютном пространстве.

Из всего сказанного в данном замечании можно сделать вывод, что соотношение (19) определяет связь абсолютного, переносного и относительного движения материальной точки в другой форме. Эта связь формулируется следующим образом.

Абсолютное движение материальной точки может быть представлено суммой абсолютного движения 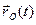точки отсчета подвижного пространства и суперпозиции (21) двух движений — относительного движения (20) материальной точки и вращения (23) подвижного пространства вокруг точки отсчета .