
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примечание. В дальнейшем, в тех случаях, когда это не будет вызывать недоразумений, в названиях векторов и слово «мгновенный» будем опускать.
В дальнейшем, в тех случаях, когда это не будет вызывать недоразумений, в названиях векторов  и
и  слово «мгновенный» будем опускать.
слово «мгновенный» будем опускать.
Выведем формулы для переносной скорости 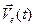 и переносного ускорения
и переносного ускорения  точки
точки  .
.
В соответствии с определением 3 переносная скорость 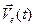 точки
точки  в момент времени
в момент времени  совпадает с абсолютной скоростью
совпадает с абсолютной скоростью  той точки
той точки  фиктивного твердого тела, которая в этот момент совпадает по своему положению с точкой
фиктивного твердого тела, которая в этот момент совпадает по своему положению с точкой  .
.
Абсолютная скорость  любой точки
любой точки  твердого тела задается формулой Эйлера
твердого тела задается формулой Эйлера
 =
= 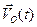 +
+ 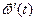

 ,
,
где  =
= 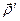 — положение точки
— положение точки  в системе
в системе  ;
; 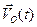 — абсолютная скорость полюса
— абсолютная скорость полюса  ;
; 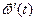 — вектор мгновенной угловой скорости фиктивного твердого тела.
— вектор мгновенной угловой скорости фиктивного твердого тела.
Поскольку по определению фиктивного твердого тела система  является для него связанной системой координат, то вектор угловой скорости
является для него связанной системой координат, то вектор угловой скорости 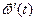 фиктивного твердого тела совпадает с вектором угловой скорости этой системы. Вектор угловой скорости системы
фиктивного твердого тела совпадает с вектором угловой скорости этой системы. Вектор угловой скорости системы  , согласно определению 4, является вектором переносной мгновенной угловой скорости
, согласно определению 4, является вектором переносной мгновенной угловой скорости  . Следовательно,
. Следовательно,  .
.
Кроме того, согласно определению 3 положение 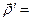
 точки
точки  совпадает в момент времени
совпадает в момент времени  с положением
с положением  точки
точки  , которое, в свою очередь, на относительном движении совпадает с
, которое, в свою очередь, на относительном движении совпадает с  =
= 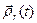 .
.
Поэтому, подставляя  и
и  =
= 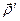 =
=  =
= 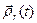 в выражение для скорости
в выражение для скорости  и учитывая, что согласно определению 3 переносная скорость
и учитывая, что согласно определению 3 переносная скорость 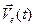 точки
точки  совпадает со скоростью
совпадает со скоростью  точки
точки  , окончательно находим
, окончательно находим
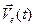 =
= 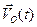 +
+  . (8)
. (8)
Действуя аналогично, по определению 3 получим выражение для переносного ускорения  точки
точки  , используя формулу Ривальса для ускорения точек твердого тела
, используя формулу Ривальса для ускорения точек твердого тела
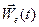 =
= 
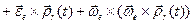 . (9)
. (9)
Здесь  =
= 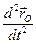 =
= 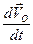 — абсолютное ускорение точки
— абсолютное ускорение точки  ;
;  — вектор мгновенной угловой скорости переносного движения;
— вектор мгновенной угловой скорости переносного движения;  — вектор мгновенного углового ускорения подвижной системы координат
— вектор мгновенного углового ускорения подвижной системы координат  , определяемый по вектору
, определяемый по вектору  по формуле (7);
по формуле (7);  =
=  — радиус-вектор точки
— радиус-вектор точки  в момент времени
в момент времени  относительно полюса
относительно полюса  подвижной системы, заданный проекциями на подвижные оси.
подвижной системы, заданный проекциями на подвижные оси.
Дата добавления: 2015-04-15; просмотров: 226; Мы поможем в написании вашей работы!; Нарушение авторских прав |