Ordm;. Связь углов Эйлера и их производных.

Обратимся к правилам ввода углов Эйлера для задания ориентации подвижной системы координат в абсолютном пространстве.

Напомним кинематическую схему

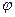
Углы вводились последовательными поворотами:

– на угол вокруг третьей оси (ось с направляющим ортом );

– на угол вокруг линии узлов, совпадающей с тем положением в плоскости, образованной первой и второй осью, которое (положение) займет первая ось после поворота на угол ; орт этой оси обозначался , причем = ;

– на угол 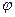вокруг третьей оси, которая является неподвижной в теле; направляющий орт этой оси совпадает с ортом .

Такие последовательные повороты можно рассматривать как три составляющих движения:

– первое движение — это вращение системы вокруг оси = относительно абсолютной системы ;

– второе движение — это вращение системы вокруг оси относительно первой подвижной системы ;

– третье движение — это вращение твердого тела вокруг оси относительно второй подвижной системы .

Таким образом, каждое составляющее движение является элементарным вращением вокруг одной оси, неподвижной в предшествующей системе координат.

Как было показано в кинематике твердого тела, каждое такое движение имеет вектор мгновенной угловой скорости вращения относительно предшествующей системы, коллинеарный оси вращения. Причем проекция его на эту ось совпадает с производной по времени от угла поворота, т.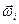е. = , где — орт оси поворота, — угол поворота, = , . Применяя приведенные здесь рассуждения к углам Эйлера, будем иметь

= , = = , =.

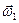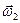Обозначим 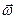— вектор мгновенной угловой скорости твердого тела относительно абсолютного пространства. А тогда согласно теореме о сложении угловых скоростей можем записать

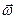= = + +. (1)

Будем смотреть на это соотношение как на векторное дифференциальное уравнение относительно углов ориентации , , 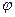при заданном векторе угловой скорости .

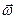Уравнение (1) называется векторным кинематическим уравнением Эйлера.

Запишем его в проекциях на связанные оси. Для этого последовательно умножим скалярно на орты , , обе части равенства (1).

Учтем, что

( , , ( , ,

( , , ( , ,

( , , ( , ,

= .

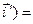
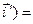
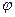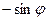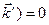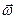В результате придем к трем равенствам

= + , = - , = + .

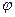Разрешая относительно производных , , , получим систему трех дифференциальных уравнений первого порядка, записанную в нормальной форме:

= , = - , = - . (2)

Система уравнений (2) называется кинематическими уравнениями Эйлера.

Они являются нелинейными дифференциальными уравнениями относительно функций , , , 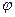если считать в них , , заданными функциями времени.