Ordm;. Кинематические уравнения Пуассона.

Откажемся от определения ориентации твердого тела через угловые параметры и будем вычислять его ориентацию по матрице перехода от связанной системы координат к абсолютной. С этой целью выведем дифференциальные уравнения, по решениям которых могут быть построены элементы указанной матрицы.

Пусть — орт, неподвижный в абсолютном пространстве. Обозначим — его проекции на подвижные оси, в качестве которых берем оси связанной с твердым телом системы координат.

Тогда можем записать

= .

Продифференцируем по данное равенство. В результате получим векторное уравнение следующего вида

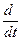
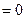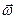
= + . (1)

При дифференцировании учли, что — орт, неподвижный в абсолютном пространстве, задается проекциями на подвижные оси. Поэтому для его производной справедлива формула (11) из §2, п.2º. Поскольку

= , = ,

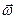где , , — орты связанной системы координат, то, проектируя (1) на оси , , , придем к следующей системе

. (2)

Уравнения (2) называются уравнениями Пуассона. Это линейные дифференциальные уравнения относительно неизвестных функций .

Матрица коэффициентов в них имеет вид

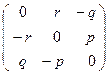= . (3)

Она является кососимметрической матрицей.

Если обозначить через вектор-столбец

= ,

то система (2) в матричном виде запишется так:

= , (4)

где матрица задается формулой (3).

В задаче Дарбу матрица является известной матричной функцией времени.

Выведем теперь дифференциальные уравнения для матрицы ориентации твердого тела.

В качестве вектора последовательно возьмем орты , , абсолютной системы координат. Поскольку координаты орта совпадают с элементами первой строки матрицы , орта — с элементами второй строки, орта — с элементами третьей строки, то можно обозначить

= , = , = ,

где — вектор-строка с номером 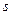в матрице ориентации :

, , .

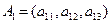Тогда система (4) для векторов , , запишется в виде

= , = , = . (5)

Объединяя эти три системы, приходим к следующему матричному дифференциальному уравнению для транспонированной матрицы :

= . (6)

Уравнение (6) — это дифференциальное уравнение Пуассона для матрицы ориентации.

По существу, уравнение (6) образует систему девяти линейных дифференциальных уравнений первого порядка относительно элементов матрицы ориентации твердого тела. Эта система не зависит явно от углов ориентации. Тем самым она не зависит от выбора угловых параметров ориентации и не зависит от диапазона допустимых значений таких углов. Матричное дифференциальное уравнение (6) не вырождается ни при каких значениях матрицы .

Таким образом, кинематическое уравнение Пуассона (6) не имеет тех недостатков, о которых говорилось в п.1º.

3º. Решение задачи Дарбу.

Ясно, что задача Дарбу будет решена, если построим решение задачи Коши для системы уравнений (6) с начальными условиями:

при .

Здесь — заданное значение матрицы ориентации при .

Матричное уравнение (6) эквивалентно системе трех уравнений (5) для векторов 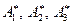. Напомним, что 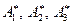суть столбцы транспонированной матрицы .

Каждое из уравнений (5) с точностью до обозначений искомых функций , и совпадает с уравнением (4).

Поэтому решения каждого уравнения (5) могут быть получены на основе интегрирования уравнения (4).

Покажем, как построить матрицу через решения уравнения Пуассона (4). Сначала отметим основные свойства решений системы (4).

1. Система (4) имеет первый интеграл .

Утверждение легко проверяется непосредственным дифференцированием функции * , вычисленной на решениях системы (4). Данный интеграл выражает собой условие того, что длина вектора не меняется при движении системы.

Нас будут интересовать только такие решения системы (4), на которых 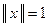, т.е. * .

2. Если и — два частных решения системы (4), то вектор

(7)

является решением системы (4).

Здесь под , , понимаем вектор

= , (8)

координаты которого в связанной системе совпадают с элементами соответствующего вектора-столбца

= .

Действительно, система (4) в обозначениях (8) примет вид

. (9)

Тогда, если , — решения системы (9), то можно записать

, . (10)

Покажем, что

(11)

является решением системы (9). Дифференцируя (11), получим

.

Заменим , , правыми частями равенств (10)

.

Раскрываем правую часть по формуле двойного векторного произведения:

.

Сравнивая с (9), куда следует подставить , видим, что — решение уравнения (9).

3. Если и — два частных решения системы (4), то при любых справедливо равенство

.

Здесь и - векторы, построенные через решения и по формуле (8). В справедливости свойства легко убедиться, если продифференцировать скалярное произведение и учесть соотношения (10).

Из доказанных свойств 1,2,3 вытекает следующее.

4. Для построения матрицы ориентации твердого тела достаточно получить два взаимно ортогональных решения и системы (9) (или системы (4)), удовлетворяющих условиям

=1, =1, .

Действительно, построим решение системы (4) с начальными условиями, совпадающими в момент времени с направляющими косинусами вектора абсолютной системы координат в связанной. Очевидно, такое решение будет определять положение вектора в связанной системе в любой момент времени .

Другими словами, компоненты решения будут являться элементами первой строки матрицы в любой момент времени .

Затем возьмем в качестве начальных условий в момент направляющие косинусы вектора абсолютной системы координат в связанной системе и по ним построим решение системы уравнений (4).

Тогда компоненты этого решения будут давать положение вектора в связанной системе в любой момент времени и совпадать с элементами второй строки матрицы .

В силу свойства 2 решений системы (4) вектор , определяемый по векторам и согласно формуле

, (12)

является ее решением. Иначе говоря, компоненты вектора при любых будут совпадать с элементами третьей строки матрицы ориентации . В (12) вектора и строятся через решения и системы (4) по формуле (8).

В итоге, после проведения описанных действий, получаем решение матричного уравнения Пуассона (6) в виде матрицы :

.

Здесь и — решения системы (4) с указанными выше начальными условиями.

Если компоненты столбца обозначим , , а столбца — , , то элементы третьего столбца матрицы (их обозначим 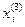, ) связаны с ними следующими соотношениями:

, , .