
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ordm;. Общая схема построения кинематических уравнений Эйлера.
Вывод кинематических уравнений Эйлера, данный в п.1º, позволяет сформулировать общую схему построения кинематических уравнений, связывающих вектор угловой скорости 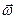 с любыми другими углами ориентации и их производными по времени.
с любыми другими углами ориентации и их производными по времени.
Общая схема построения этих уравнений такова.
1. В соответствии с заданной последовательностью поворотов вокруг координатных осей при вводе углов ориентации определяется последовательность  угловых скоростей
угловых скоростей 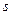 -ой системы координат относительно (
-ой системы координат относительно (  )-ой системы.
)-ой системы.
Вектор  вычисляется по формуле
вычисляется по формуле
 =
= 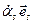 ,
,
где  — орт той оси, номер которой указывается в схеме на этапе ввода угла
— орт той оси, номер которой указывается в схеме на этапе ввода угла  . Эта ось является общей для систем с номером
. Эта ось является общей для систем с номером 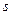 и
и  . Вокруг нее осуществляется поворот на угол
. Вокруг нее осуществляется поворот на угол  при построении
при построении 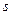 -ой системы координат.
-ой системы координат.
Таким образом, в кинематической схеме вместе с углами ориентации

указываются вектора  =
= 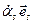 , где
, где  — орт той оси, номер которой задан в схеме.
— орт той оси, номер которой задан в схеме.
2. Применяется теорема о сложении угловых скоростей, и для вектора угловой скорости твердого тела записывается равенство
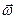 =
=  =
= 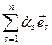 .
.
Оно рассматривается как векторное кинематическое уравнение, связывающее проекции вектора 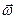 на оси выбранной системы отсчета с введенными углами ориентации и их производными.
на оси выбранной системы отсчета с введенными углами ориентации и их производными.
Уравнение можно проектировать на связанные оси (или любые другие) и получать явную зависимость проекций вектора 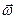 на выбранные оси от углов ориентации и их производных.
на выбранные оси от углов ориентации и их производных.
Покажем реализацию данного алгоритма построения кинематических уравнений на примере самолетных углов.
Для самолетных углов схема их ввода такова:
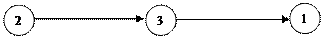 |


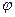
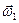 =
=  ,
, 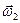 =
=  ,
,  =
= 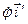 .
.
Эта схема дополнена указанием угловых скоростей элементарных вращений. В ней  =
= 
 +
+ 
 . Тогда по теореме сложения угловых скоростей записываем векторное кинематическое уравнение
. Тогда по теореме сложения угловых скоростей записываем векторное кинематическое уравнение
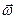 =
=  +
+  +
+ 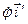 . (3)
. (3)
Проектируем векторное уравнение (3) на связанные оси. Умножим его последовательно скалярно на орты  ,
,  ,
,  и учтем следующие соотношения, полученные при построении матрицы ориентации через самолетные углы:
и учтем следующие соотношения, полученные при построении матрицы ориентации через самолетные углы:
(  ,
, 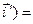
 , (
, (  ,
,  ,
,
(  ,
,

 , (
, (  ,
,
 ,
,
(  ,
, 

 , (
, (  ,
, 
 .
.
В результате придем к трем скалярным уравнениям
 =
= 
 +
+  ,
,  =
= 

 +
+ 
 ,
,  =
= 

 +
+ 
 .
.
Отсюда, разрешая относительно производных  ,
,  ,
,  , находим кинематические уравнения для самолетных углов:
, находим кинематические уравнения для самолетных углов:
 =
= 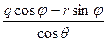 ,
,  =
= 
 +
+ 
 ,
,  =
=  -
- 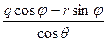
 .
.
Дата добавления: 2015-04-15; просмотров: 365; Мы поможем в написании вашей работы!; Нарушение авторских прав |