
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Элементы линейной алгебры и аналитической геометрии
Контрольных работ по дисциплине
«математика»
для студентов заочной формы обучения
направления подготовки 051000. 62 Профессиональное обучение (по отраслям)
профиля подготовки «Энергетика»
профиля подготовки «Информатика и вычислительная техника»
Екатеринбург
РГППУ
Задания и методические указания к выполнению контрольных работ по дисциплине «Математика». Екатеринбург, ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», 2012. 48с.
Авторы канд. физ.-мат. наук С.Д. Филиппов
канд. физ.-мат. наукА.В. Шитиков
ст. преподаватель Т.А. Серова
Одобрены на заседании кафедры высшей математики.
Протокол от 02.10.2012 № 2
Заведующий кафедрой Е.А.Перминов
Рекомендованы к печати методической комиссией МаИ РГППУ.
Протокол от 05.10.2012 №2
Председатель методической
комиссии МаИ РГППУ А.В.Песков
ФГАОУ ВПО «Российский
государственный профессионально-
Педагогический университет», 2012
Цель контрольных работ – закрепление и проверка знаний, полученных студентами в процессе самостоятельного изучения учебного материала по данной дисциплине, а также выявление их умения применять полученные знания на практике.
Указания к выполнению контрольных работ
При выполнении контрольных работ необходимо руководствоваться следующими требованиями:
1. Вариант контрольной работы выбирать по последней цифре номера зачетной книжки.
2. Каждую контрольную работу следует выполнять в отдельной тетради.
3. На обложке тетради должны быть ясно написаны название дисциплины, номер контрольной работы, фамилия студента, его инициалы, номер группы и шифр специализации, шифр зачетной книжки.
4. В начале работы должен быть указан номер варианта задания.
5. Перед решением задачи должно быть полностью приведено ее условие.
6. Решение задач следует сопровождать необходимыми формулами, развернутыми расчетами и краткими пояснениями.
7. В конце работы должна стоять подпись студента с указанием даты ее выполнения.
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ ЗАДАНИЙ
Элементы линейной алгебры и аналитической геометрии
11-20. В пирамиде SABC: треугольник АВС – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S. Сделать чертеж. Найти:
1) длину ребра АВ;
2) угол между ребрами АВ и AS;
3) угол наклона ребра AS к основанию пирамиды;
4) площадь основания пирамиды;
5) объем пирамиды;
6) уравнение прямой АВ;
7) уравнение плоскости АВС;
8) проекцию вершины S на плоскость АВС;
9) длину высоты пирамиды.
11. А(-2;0;0); В(0;3;0); C(0;0;1); S(0;2;3).
12. А(4;0;0); В(0;-8;0); C(0;0;2); S(4;6;3).
13. А(-2;0;0); В(0;6;0); C(0;0;2); S(-1;6;4).
14. А(1;0;0); В(0;2;0); C(0;0;2); S(1;1;4).
15. А(-3;0;0); В(0;-2;0); C(0;0;1); S(-2;-1;3).
16. А(6;0;0); В(0;-3;0); C(0;0;2); S(4;-3;4).
17. А(3;0;0); В(0;-6;0); C(0;0;1); S(1;-3;3).
18. А(-4;0;0); В(0;4;0); C(0;0;2); S(-2;4;3).
19. А(-6;0;0); В(0;2;0); C(0;0;3); S(-3;2;5).
20. А(-1;0;0); В(0;5;0); C(0;0;2); S(-1;3;4).
51-60. Дана система линейных уравнений: 
Доказать ее совместность и решить тремя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) по правилу Крамера.
51.  52.
52. 
53.  54.
54. 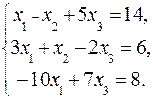
55. 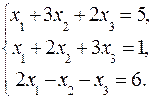 56.
56. 
57. 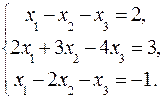 58.
58. 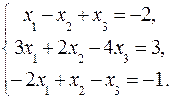
59. 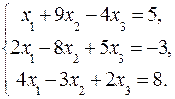 60.
60. 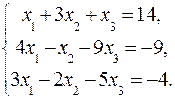
71-80. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А.
71. 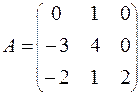 72.
72. 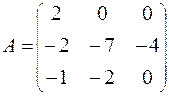
73. 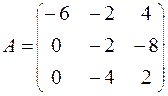 74.
74. 
75. 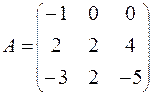 76.
76. 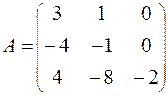
77. 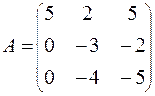 78.
78. 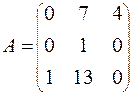
79. 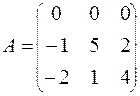 80.
80. 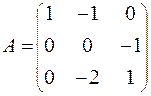
91-100. Дано комплексное число a. Требуется: 1) записать число a в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3+a=0.
91. 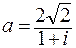 . 92.
. 92.  . 93.
. 93.  .
.
94. 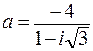 .95.
.95. 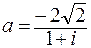 . 96.
. 96. 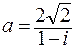 .
.
97. 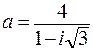 . 98.
. 98. 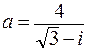 . 99.
. 99. 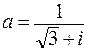 . 100.
. 100.  .
.
111-120. Найти пределы функций, не пользуясь правилом Лопиталя.
111. а) 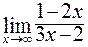 ; б)
; б) 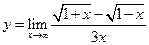 ;
;
в) 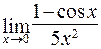 ; г)
; г) 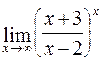 .
.
112. а) 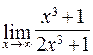 ; б)
; б) 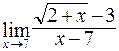 ;
;
в)  ; г)
; г) 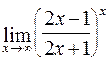 .
.
113. а) 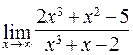 ; б)
; б) 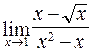 ;
;
в) 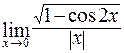 ; г)
; г) 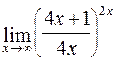 .
.
114. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 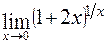 .
.
115. а) 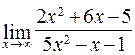 ; б)
; б) 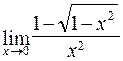 ;
;
в) 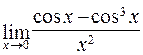 ; г)
; г) 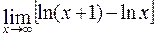 .
.
116. а)  ; б)
; б) 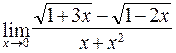 ;
;
в)  ; г)
; г) 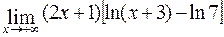 .
.
117. а)  ; б)
; б) 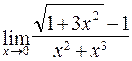 ;
;
в) 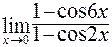 ; г)
; г) 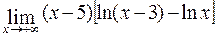 .
.
118. а) 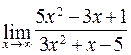 ; б)
; б) 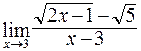 ;
;
в) 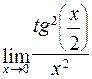 ; г)
; г)  .
.
119. а) 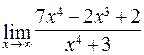 ; б)
; б) 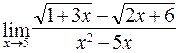 ;
;
в) 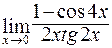 ; г)
; г)  .
.
120. а) 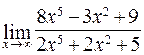 ; б)
; б) 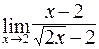 ;
;
в) 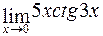 ; г)
; г) 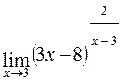 .
.
Дата добавления: 2015-04-16; просмотров: 308; Мы поможем в написании вашей работы!; Нарушение авторских прав |