Задание 441 – 450

Вычислить определённый интеграл с точностью 0,001, Разложим подынтегральную функцию в ряд, а затем проинтегрируем её почленно.

.

Используя разложение в ряд Маклорена функции

, запишем разложение

Проинтегрировав, получим:

Значение интеграла (по теореме Лейбница) соответствует сумме с точностью 0,001.

Шестое слагаемое , поэтому взято пять слагаемых.

Типовые задачи по теме «Ряды» рассматриваются в учебном пособии П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах, ч. , гл. ,§§1-6.

Задание 451 – 460.

Найти три первых отличных от нуля члена разложения в степенной ряд решения 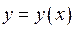дифференциального уравнения 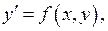удовлетворяющего данному условию

Используем разложение искомой функции в ряд Тейлора около точки .

В нашем примере т.е. первый член ряда обращается в ноль.

Из заданного дифференциального уравнения

Поэтому второй член ряда имеет вид . Чтобы найти третий член ряда продифференцируем обе части нашего уравнения

И поэтому следующий член ряда равен . Аналогично

Третий ненулевой член ряда

Окончательно:

Интегрирование дифференциальных уравнений с помощью рядов рассматривается в учебном пособии П.Е.Данко, А.Г.Попов, Т.М.Кожевникова. Высшая математика в упражнениях и задачах, ч. гл. , §4.