Задание 191 – 200

Исследовать методами дифференциального исчисления функцию и построить её график.

Рассмотрим свойства функции:

1. Область определения:

2. Чётностьь, нечётность функции:

Функция общего вида.

3. Асимптоты.

а) Так как , то прямая является вертикальной асимптотой:

б) – наклонная асимптота.

Найдём

Найдём

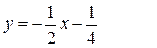– уравнение наклонной асимптоты.

4. Найдём точки экстремума и интервалы монотонности функции:

Так как то действительных корней нет, значит, нет точек экстремума.

Производная на всей области определения, значит функция

убывает.

5. Точки пересечения с координатными осями

а) с осью при ,

б) с осью при .

Используя исследование функции, строим график (схематично).

Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.