Теория вероятностей и математическая статистика

521. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) студент знает только два вопроса; в) студент знает только один вопрос.

522. В каждой из двух урн находится 5 белых и 10 черных шаров. Из первой урны во вторую переложили наудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.

523. Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадёт в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.

524. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,7. Найти вероятность того, что в 1600 испытаниях событие наступит 1100 раз.

525. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равно 0,9, второе – 0,95 и третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) только два устройства; в) все три устройства.

526. Вероятность наступления события в каждом из одинаковых независимых испытаний равна 0,07. Найти вероятность того, что в 1400 испытаниях событие наступит 78 раз.

527. В партии из 1000 изделий имеется 10 дефектных. Найти вероятность того, что среди 50 изделий наудачу взятых из этой партии ровно 3 окажется дефектными.

528. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 225 испытаниях событие наступит не менее 175 и не более 190 раз.

529. На трех станках при одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30%, на третьем – 60% деталей. Вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке; 0,8, если на втором станке; 0,9 – если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.

530. Вероятность того, что изготовленная на первом станке деталь будет первосортной, равна 0,7. При изготовлении такой детали на втором станке эта вероятность равна 0,8. На первом станке изготовлены 2 детали, а втором – 3. Найти вероятность того, что все детали первосортные.

531-540. Дискретная случайная величина Х может принимать только два значения x₁ и x₂, причём . Известны вероятность p₁ возможного значения x₁, математическое ожидание M(X) и дисперсия D(X). Найти закон распределения этой случайной величины.

531. p₁=0,1 M(X)=3,9 D(X)=0,09

532. p₁=0,3 M(X)=3,7 D(X)=0,21

533. p₁=0,5 M(X)=3,5 D(X)=0,25

534. p₁=0,7 M(X)=3,3 D(X)=0,21

535. p₁=0,9 M(X)=3,1 D(X)=0,09

536. p₁=0,9 M(X)=2,2 D(X)=0,36

537. p₁=0,8 M(X)=3,2 D(X)=0,16

538. p₁=0,6 M(X)=3,4 D(X)=0,24

539. p₁=0,4 M(X)=36 D(X)=0,24

540. p₁=0,2 M(X)=3,8 D(X)=0,16

541-550. Случайная величина Х задана функцией распределения F(x). Найти плотность распределения, математическое ожидание и дисперсию случайной величины.

541. 542.

543. 544.

545. 546.

547. 548.

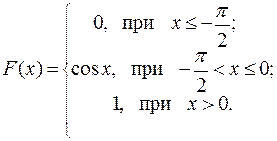
549.

550.

551-560. Известны математическое ожидание а и среднее квадратическое отклонение σ нормально распределенной случайной величины х. Найти вероятность попадания этой величины в заданный интервал (α; β).

551. а=10, σ=4, α=2, β=13.

552. а=9, σ=5, α=5, β=14.

553. а=8, σ=1, α=4, β=9.

554. а=7, σ=2, α=3, β=10.

555. а=6, σ=3, α=2, β=11.

556. а=5, σ=1, α=1, β=12.

557. а=4, σ=5, α=2, β=11.

558. а=3, σ=2, α=3, β=10.

559. а=2, σ=5, α=4, β=9.

560. а=2, σ=4, α=6, β=10.

571-580. Найти доверительный интервал для оценки математического ожидания a нормального распределения с надёжностью 0,95, зная выборочную среднюю , объем выборки n и среднее квадратическое отклонение σ.

571. 75,17 n=36 σ =6

572. 75,16 n=49 σ =7

573. 75,15 n=64 σ =8

574. 75,14 n=81 σ =9

575. 75,13 n=100 σ =10

576. 75,12 n=121 σ =11

577. 75,11 n=144 σ =12

578. 75,10 n=169 σ =13

579. 75,09 n=196 σ =14

580. 75,08 n=225 σ =15