Двойные и криволинейные интегралы

351-360.Вычислить двойные интегралы по области D.

351. , где D – область, ограниченная линиям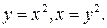

352. , где D – область, ограниченная линиями

353. , где D – область, ограниченная линиями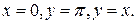

354. , где D – область, ограниченная линиями

355. 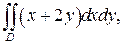где D – область, ограниченная линиями

356. , где D – область, ограниченная линиями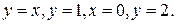

357. 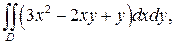где D – область, ограниченная линиями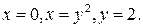

358. где D – область, ограниченная линиями

359. , где D – область, ограниченная линиями

360. 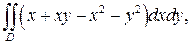где D – область, ограниченная линиями

.

371 – 380. Вычислить криволинейные интегралы

371. где L – контур треугольника, образованного осями координат и прямой 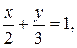в положительном направлении, т.е. против движения часовой стрелки.

372. где L – дуга параболы от точки О (0;0) до точки

А(2;4).

373. где L – контур прямоугольника, образованного прямыми

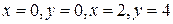в положительном направлении (против часовой стрелки).

374. вдоль кривой .

375. вдоль кривой от точки О (0;0) до точки А(1;1).

376. вдоль отточки О (0;0) до точки А(1;1).

377. , где L – четверть окружности 0 , против часовой стрелки.

378. , где L – первая арка циклоиды 0 .

379. 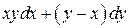вдоль линии от точки О (0;0) до точки А(1;1).

380. вдоль отрезка ОА, О (0;0), .

Ряды

421-430. Исследовать сходимость числового ряда.

421. . 422. 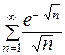. 423. . 424. . 425. 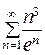. 426. .

427. . 428. . 429. . 430. .

431-440. Найти интервал сходимости степенного ряда.

431. . 432. . 433. .

434. 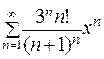. 435. . 436. .

437. . 438. . 439. .

440. .

441-450. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.

441. 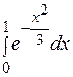. 442. . 443. .

444. . 445. . 446. .

447. . 448. . 449. 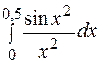. 450. .

451 – 460.Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения 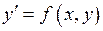, удовлетворяющего начальному условию .

451. 452.

453. 454.

455. 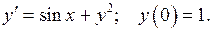456.

457. 458.

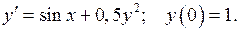
459. 460.

461 – 470.Разложить данную функцию в ряд Фурье в интервале .

461. в интервале

462. в интервале

463. в интервале

464. 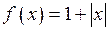в интервале

465. 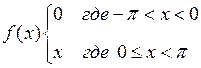в интервале

466. в интервале

467. в интервале

468. в интервале

469. в интервале

470. 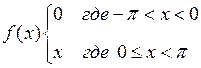в интервале