Задание 11 – 20

Для решения задач 11 – 20 рекомендуется учебное пособие

Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.

Ч.1. М.: Оникс 21 век. 2005. Гл. I –IV, стр.39 – 91.

Рассмотрим решение аналогичной задачи, взяв координаты вершины пирамиды SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).

1) Длину ребра АВ находим по формуле:

2) Угол между рёбрами 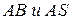найдём по формуле косинуса угла между векторами , координаты которых определяются так:

α

φ

Для решения задания 3) целесообразно решить задачу 7). Уравнение плоскости составим по уравнению

Нормальный вектор этой плоскости

4) Площадь определяем с помощью векторного произведения:

5) Объём пирамиды находится через вычисление смешанного произведения векторов Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Решите самостоятельно.

6) Уравнение прямой

Канонические уравнения прямой, вектор направляющий вектор прямой

8) Для определения проекции вершины на плоскость выполняются следующие действия:

а) составляется уравнение высоты пирамиды .

б) находится точка пересечения высоты и основания решением системы, содержащей уравнение высоты и уравнение плоскости.

Решение: вектор 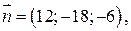удобнее взять

Он будет направляющим для По уравнению

вершина , т.е.

.

Система решается подстановкой

Подставив во второе уравнение, найдём значение , а следовательно значения

Точка - проекция точки на плоскость

9) Длину высоты пирамиды можно найти по формуле или по формуле расстояния от точки до плоскости – наиболее удобно.

Изучите формулы самостоятельно, решив задание 9).