Задание 391-400

Вычислить криволинейный интеграл по дуге 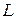линии, заданной параметрически

Тогда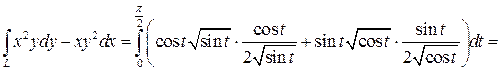

Задание 421-430

Исследовать сходимость числового ряда

‌‌‌‌‌‌‌‌‌‌‌ Для исследования данного ряда применяем признак Даламбера:

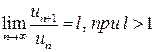· , ряд расходящийся, сходящийся, 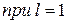нет ответа по данному признаку.

по данному условию, составим

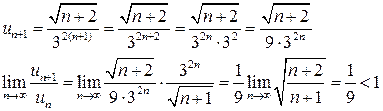
Значит данный ряд сходящийся.

Задание 431-440

Найти область сходимости степенного ряда

Прежде всего определяется радиус сходимости степенного ряда

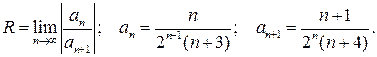
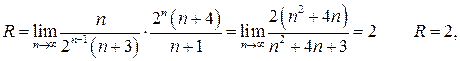
Значит интервал сходимости

На границах интервала рассматриваются числовые ряды.

При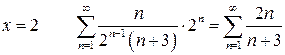

Так как предел 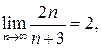то ряд расходится.

При 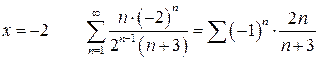–знакочередующийся ряд.

1. Рассмотрим члены ряда по абсолютной величине

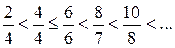
Члены ряда возрастают, значит по теореме Лейбница при 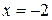ряд расходящийся.