Задание 481 – 491.

Представить 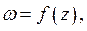где 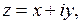в виде ; проверить, является ли она аналитической. Если да, то найти значение её производной в заданной точке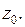

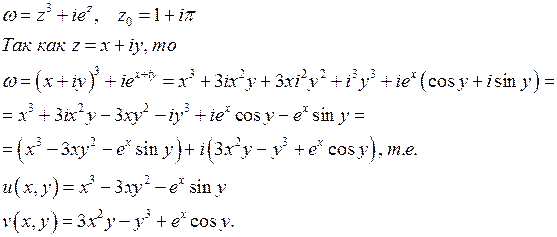
Здесь мы воспользовались формулой Эйлера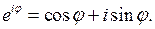

Необходимыми условиями дифференцируемости функции в точке являются условия Коши – Римана

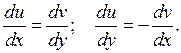
Находим частные производные

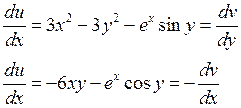
Т.е. условия Коши – Римана выполнены во всех точках комплексной плоскости. Кроме того, частные производные непрерывны всюду. Следовательно, заданная функция дифференцируема и является аналитической на всей комплексной плоскости.

Производная может быть найдена по тем же формулам, что для функций действительного переменного.

В заданной точке

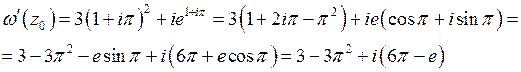
Типовые задачи по теме «Производная функции комплексного переменного» рассматривается в учебном пособии П.Е.Данко, А.Г.Попов, Т.М.Кожевникова. Высшая математика в упражнениях и задачах, ч. гл.VII, §§1,2.