Задание 461 – 470

Разложить данную функцию 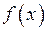в ряд Фурье в интервале

Рядом Фурье периодической функции 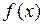с периодом 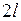, определённой на сегменте 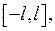называется ряд

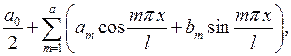где (1)

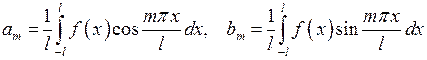
В случае, когда чётная функция, её ряд Фурье содержит только свободный член и косинусы, т.е.

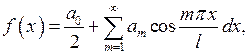
В случае, когда нечётная функция, её ряд Фурье содержит только синусы, т.е.

Если ряд (1) сходится то его сумма 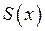есть периодическая функция с периодом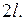

Теорема Дирихле. Пусть функция 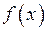на сегменте 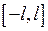имеет конечное число экстремумов и является непрерывной за исключением конечного числа точек разрыва рода. Тогда ряд Фурье этой функции сходится в каждой точке сегмента 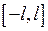и сумма 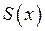этого ряда:

1) 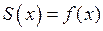во всех точках непрерывности функции 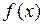, лежащих внутри сегмента ;

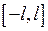2) , где - точка разрыва I рода функции ;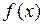

3) 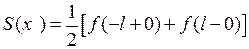на концах промежутка , т.е. при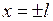

Разложить в ряд Фурье функцию 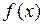, заданную в интервале уравнением .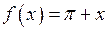

Графиком этой функции в интервале является отрезок, соединяющий точки 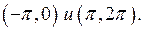Сумма ряда Фурье является периодической функцией с периодом и совпадает с функцией 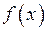в интервале .

Определяем коэффициенты ряда Фурье . Сначала находим

Второй интеграл равен нулю как интеграл от нечётной функции, взятый по интервалу, симметричному относительно начала координат. Таким образом,

Далее, находим коэффициенты 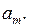Имеем

Нетрудно видеть, что оба интеграла равны нулю (подъинтегральная функция второго интеграла является нечётной как произведение чётной функции на нечётную). Итак,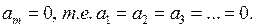

Найдём теперь коэффициенты

Первый интеграл равен нулю. Подъинтегральная функция второго интеграла является чётной как произведение двух нечётных функций. Таким образом,

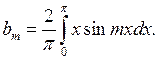
Интегрируя по частям, получим

Следовательно, разложение функции в ряд Фурье имеет вид:

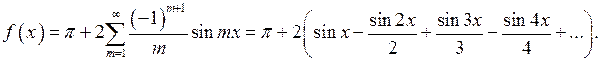
Ряды Фурье рассматриваются в учебном пособии П.Е.Данко, А.Г.Попов, Т.М.Кожевникова. Высшая математика в упражнениях и задачах, ч. гл.3, §8.