КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Точечные статистики
Пусть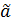 
является точечной оценкой параметра 
.
К точечным оценкам числовых характеристик предъявляются следующие требования:
1. Состоятельность –при увеличении числа опытов оценка сходится по вероятности к оцениваемому параметру, т.е. выполняется условие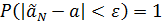 
при увеличении объема выборки 
.
2. Несмещенность – математическое ожидание оценки равно оцениваемому параметру, т.е. при увеличении объема выборки ее математическое ожидание стремится к оцениваемому параметру: 
при увеличении .
3. Эффективность –несмещенная оценкадолжна обладать минимальной дисперсией по сравнению с другими оценками, т.е. 
.
Все точечные оценки можно разделить на три группы - средние статистики, статистики рассеяния и статистики отклонения формы распределения.
Средние статистики.Средние статистики определяют центр распределения случайной величины, около которого группируется большая ее часть, т.е. измеряют центральную тенденцию выборки. Средние величины отражают закономерный результат воздействия главных возмущающих факторов.
Выборочное среднее (среднее арифметическое). Является наиболее часто употребляемой оценкой математического ожидания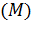 
, вычисляется как
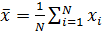(4.1)
Медиана. Оценка вычисляется как среднее значение вариационного ряда. Медиана делит вариационный ряд на две, равные по объему выборки, в силу чего равновероятно, что случайная величина будет больше или меньше значения медианы.
Квантиль выборки представляет собой число хр, ниже которого находится р-я часть (доли) выборки.
Например, квантиль 0,25 для некоторой переменной - это такое значение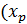 
), ниже которого находится 25% значений переменной.
Аналогично квантиль 0,75 - это такое значение, ниже которого попадают 75% значений выборки.
Квартили (от слова кварта - четверть). Нижняя и верхняя квартили, равны соответственно 25-й и 75-й процентилям распределения.
25-я процентиль переменной - это значение, ниже которого располагаются 25% значений переменной. Аналогично, 75-я процентиль равна значению, ниже которого расположено 75% значений переменной.
Итак, три точки: нижняя квартиль, медиана и верхняя квартиль делят выборку на 4 равные части. При этом, 1/4 наблюдений лежит между минимальным значением и нижней квартилью; 1/4 - между нижней квартилью и медианой; 1/4 - между медианой и верхней квартилью; 1/4 - между верхней квартилью и максимальным значением выборки.
Мода. Оценка 
вычисляется как значение выборки, наблюдаемое наибольшее число раз. На графике кривой функции плотности распределения мода соответствует точке локального максимума.
В случае симметричного распределения медиана совпадает с модой и математическим ожиданием.
Статистики рассеяния.Статистики рассеяния отражают результат воздействия возмущающих факторов.
Выборочная дисперсия. На первый взгляд она должна оцениваться формулой
,
Но эта оценка получается несколько смещенной:
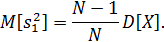
Поэтому для оценки дисперсии используется несмещенная оценка:
.
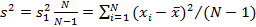Уменьшение знаменателя на единицу непосредственно связано с тем, что величина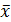 
, относительно которой берутся отклонения, сама зависит от объема выборки. Каждая величина, зависящая от элементов выборки и входящая в формулу, называется связью.В статистике доказывается, что знаменатель выборочной дисперсии всегда равен разности между объемом выборки и числом связей 
, наложенных на эту выборку. Эта разность
называется числом степеней свободы выборки. В практических вычислениях для оценки дисперсии часто используется более удобная формула:
Преимущество этой формулы в том, что в ней нет операций вычитания близких чисел, приводящих к потере точности.
Обычно при 
можно считать, что 
.
Выборочное среднеквадратическое отклонение. Дисперсия случайной величины имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Поэтому часто используется среднее квадратическое отклонение (СКО или стандарт), равное квадратному корню из дисперсии и обозначаемое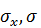 
, а его оценка вычисляется как
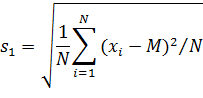
Коэффициент вариации. Его оценка вычисляется как 
Принято считать, что при значениях оценки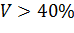 
разброс значений исследуемого параметра значителен, а при 
наблюдения неоднородны. При значениях 
, близких к 0, коэффициент не используют. Оценка используется обычно для сравнения двух выборок.
Размах варьирования. Оценка 
вычисляется как разница между максимальным и минимальным значениями в выборке. Является упрощенной оценкой рассеяния.
Статистики отклонения формы распределенияиспользуются для характеристики вида кривой распределения.
Коэффициент асимметриислужит для характеристики асимметрии (скошенности) распределения. Если распределение симметрично относительно математического ожидания, то все центральные моменты[1] нечетного порядка (если они существуют), равны нулю. Поэтому наиболее логично принять 3-й центральный момент, а чтобы получить безразмерную характеристику, его делят на куб среднего квадратического отклонения. Оценка асимметрии
,где 
– третий центральный момент, вычисляется как
| f(x) |
| x |
| Mo2 |
| A2<0 |
| A1>0 |
| Mo1 |
.Коэффициент асимметрии характеризует отклонение функции плотности расРисунок 4.1- К понятию коэффициента асимметрии
пределения от симметричной формы относительно выборочного среднего значения 
. Если в вариационном ряду преобладают варианты, меньшие , то асимметрия называется левосторонней, при этом ,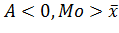 
, при значении 
асимметрия называется правосторонней, в этом случае справедливо соотношение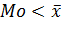 
. Для симметричного распределения справедливо 
Эксцесс (коэффициент крутости). Эксцесс характеризует форму вершины кривой плотности распределения. Эксцесс указывает, насколько плотность распределения более заострена, или наоборот, полога по сравнению с плотностью нормального распределения.
| f(x) |
| x |
| E<0 |
| E=0 |
| E>0 |
Рисунок 4.2 - К понятию коэффициента эксцесса
Оценка вычисляется как
,
где 
- оценка центрального выборочного момента 4-го порядка рассчитывается по формуле
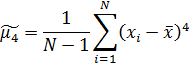
Эксцесс характеризует форму вершины кривой плотности распределения. Эксцесс указывает, насколько плотность распределения более заострена, или наоборот, приплюснута по сравнению с плотностью нормального распределения. Распределение считается близким к нормальному, если выборочные значения удовлетворяют условию 
Коэффициент асимметрии и эксцесс нормально распределённой случайной величины равны нулю.
Дата добавления: 2014-11-13; просмотров: 162; Мы поможем в написании вашей работы!; Нарушение авторских прав |